
分析 首先过点O作OH⊥AB于点H,连接OA,OB,由⊙O的周长等于6πcm,可得⊙O的半径,又由圆的内接多边形的性质,即可求得答案.
解答 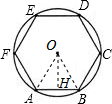 解:如图,过点O作OH⊥AB于点H,连接OA,OB,
解:如图,过点O作OH⊥AB于点H,连接OA,OB,
∴AH=$\frac{1}{2}$AB,
∵⊙O的周长等于6πcm,
∴⊙O的半径为:3cm,
∵∠AOB=$\frac{1}{6}$×360°=60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA=3cm,
∴AH=$\frac{3}{2}$cm,
∴OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=$\frac{3\sqrt{3}}{2}$(cm),
∴S正六边形ABCDEF=6S△OAB=6×$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$=$\frac{27\sqrt{3}}{2}$(cm2).
故答案为;$\frac{27\sqrt{3}}{2}$.
点评 本题考查的是正多边形和圆,熟知正六边形的半径与边长相等是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
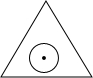 如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.
如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差是44 | B. | 众数是61 | C. | 平均数是62 | D. | 中位数是61 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ac<bc | B. | bc>c2 | C. | ab>b2 | D. | a2<b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
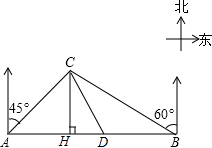 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com