练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知x-6y=5，那么x2-6xy-30y的值是25．

    分析 原式后两项提取公因式，把已知等式变形后代入计算即可求出值．

    解答 解：∵x-6y=5，即6y=x-5，
    ∴原式=x2-6y（x+5）
    =x2-（x+5）（x-5）
    =x2-x2+25=25．
    故答案为：25．

    点评 此题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．若|a|=2，$\sqrt{b}$=3，且ab＜0，则a-b=-11．

    查看答案和解析>>

    科目：初中数学 来源：2017届江西省九年级下学期第一次模拟考试数学试卷（解析版） 题型：解答题

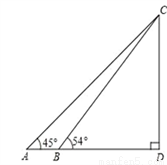
    钟楼是云南大学的标志性建筑之一，某校教学兴趣小组要测量钟楼的高度，如图，他们在点A处测得钟楼最高点C的仰角为45°，再往钟楼方向前进至点B处测得最高点C的仰角为54°，AB=7m，根据这个兴趣小组测得的数据，计算钟楼的高度CD．（tan36°≈0.73，结果保留整数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．现有两块等腰直角形三角板，如图，把其中一块三角板A′B′C′的一个锐角顶点B'放在另一块三角板ABC斜边AB的中点处，并使三角板A′B′C′绕着点B′旋转．
    （1）当两块三角板相对位置如图①，即AC与A′B′交于点D，BC与B′C′交于点E时，求证：△AB′D∽△BEB′：
    （2）当两块三角板相对位置如图②，即AC边的延长线与A′B′交于点D，BC与B′C′交于点E时，△AB′D与△BEB′还相似吗？（直接给出结论．不需证明）
    （3）在图②中，连结DE，试探究△AB′D与△B′ED是否相似，并说明理由或给出证明．
    （4）在图①中，若△ABC改为角C等于150°的等腰三角形，那么△A′B′C′只要满足∠A′B′C′=15°时，仍有△AB′D∽△BEB′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x轴上，且∠ACB=90°，AC=BC．
    （1）如图1，当A（0，-3），C（1，0），点B在第四象限时，则点B的坐标为（4，-1）；
    （2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断$\frac{OC+BD}{OA}$与$\frac{OC-BD}{OA}$哪一个是定值，并说明定值是多少？请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

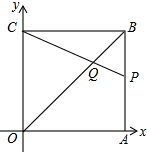    19．如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A，C分别在x，y轴的正半轴上，点Q在对角线OB上，且QO=OC，连接CQ并延长CQ交边AB于点P，则点P与Q的坐标分别为（2，4-2$\sqrt{2}$）、（$\sqrt{2}，\sqrt{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：点E为AB边上的一个动点．
    （1）如图1，若△ABC是等边三角形，以CE为边在BC的同侧作等边△DEC，连结AD．试比较∠DAC与∠B的大小，并说明理由；
    （2）如图2，若△ABC中，AB=AC，以CE为底边在BC的同侧作等腰△DEC，且△DEC∽△ABC，连结AD．试判断AD与BC的位置关系，并说明理由；
    （3）如图3，若四边形ABCD是边长为2的正方形，以CE为边在BC的同侧作正方形ECGF．
    ①试说明点G一定在AD的延长线上；
    ②当点E在AB边上由点B运动至点A时，点F随之运动，求点F的运动路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

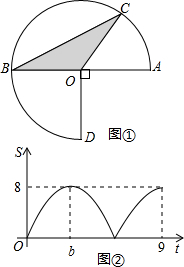    3．如图①，点C在以O为圆心，以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D，OD⊥AB．在此运动过程中，△BOC的面积S与运动时间t（秒）之间的函数图象（非抛物线）如图②所示，根据函数图象回答下列问题：
    （1）填空：a=30，b=3；
    （2）当t=5时，求∠ABC的度数及扇形OBC的面积；
    （3）当t为何值时，△BOC的面积为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知⊙O的周长等于6πcm，则它的内接正六边形面积为$\frac{27\sqrt{3}}{2}$cm3．

    查看答案和解析>>

    同步练习册答案