
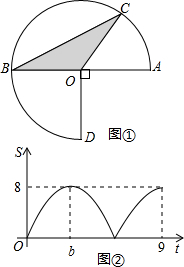
 如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:
如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:分析 (1)当 CO⊥AB时,面积最大,当C点与A,B重合时面积最小,CO两次垂直于AB,第一次时,∠AOC=90°,第二次时,∠AOC=270°,结合图象,易得出结论;
(2)由(1)得∠ABC,由圆周角定理可得∠ABC,∠BOC,结合图象易得R,利用扇形的面积公式得出结论;
(3)若△BOC的面积为4,则以BO为底的高为2,易得∠AOC=30°,150°或210°时,解得t.
解答 解:(1)由题意得:当∠AOC=90°时,第一次面积最大;当∠AOC=180°时,面积最小,
当∠AOC=270°时,面积第二次最大,
∴a=$\frac{270°}{9}$=30°,b=$\frac{9}{3}=3$,
故答案为:30,3;
(2)当t=5时,∠AOC=30t=150°,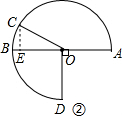
∴$∠ABC=\frac{1}{2}∠AOC=75°$,
∴∠BOC=30°,
设⊙O的半径为R,则$\frac{1}{2}$R2=8,
∴R=4,
∴S扇形OBC=$\frac{30π{•4}^{2}}{360}$=$\frac{4}{3}$π;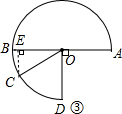
(3)作CE⊥AB于E,当$\frac{1}{2}$OB•CE=4时,即$\frac{1}{2}×4CE$=4,
∴CE=2,
在Rt△OCE中,sin∠COE=$\frac{CE}{OE}$=$\frac{1}{2}$,
∴∠COE=30°,
如图①∠AOC=30°,t=30÷30=1(秒);
如图②∠AOC=150°,t=150÷30=5(秒);
如图③∠AOC=210°,t=210÷30=7(秒);
∴当t为1秒,5秒,7秒时,△BOC的面积为4.
点评 本题主要考查圆周角定理,结合图象解决动点问题,正确识图,分清界点结合图象是解答此题的关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:单选题
图①,在边长为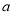 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为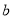 的小正方形(
的小正方形(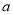 >
> 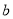 ),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )

A. (a+2b)(a-b)=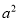 +ab-2
+ab-2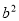
B. 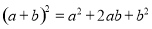
C. 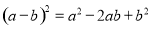
D. 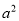 -
-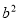 =(a+b)(a-b)
=(a+b)(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
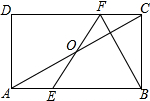 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ac<bc | B. | bc>c2 | C. | ab>b2 | D. | a2<b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com