
分析 首先利用根与系数的关系得出得出b,c是关于x的一元二次方程x2-(10-a)x+(23+$\frac{40}{a}$)=0的两个根,进而得出a的取值范围,再求出|a|+|b|+|c|的最小值.
解答 解:由题意可得:a>0,b+c=10-a,且bc=23+$\frac{40}{a}$,
所以b,c是关于x的一元二次方程x2-(10-a)x+(23+$\frac{40}{a}$)=0的两个根.
故△=(10-a)2-4(23+$\frac{40}{a}$)≥0,
a3-20a2+8a-160≥0,
即(a2+8)(a-20)≥0,
所以a≥20.
于是b+c=10-a≤-10,|b+c|≥10,从而|b|+|c|≥|b+c|≥10,
故|a|+|b|+|c|≥30,
当a=20,b=-5,c=-5时,等号成立,
即|a|+|b|+|c|的最小值为30.
点评 此题主要考查了绝对值函数的最值,得出a的取值范围是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
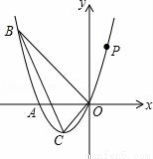
如图,已知抛物线经过点A(﹣2,0),点B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)在抛物线的BC段上,是否存在一点G,使得△GBC的面积最大?若存在,求出这个最大值及此时点G的坐标;若不存在,请说明理由;
(3)P是抛物线的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由;
(4)若点D在抛物线上,点E在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
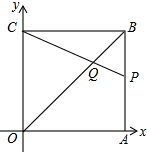 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
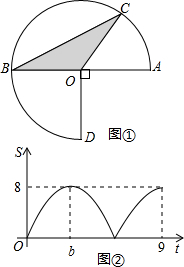 如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:
如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
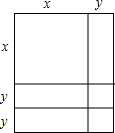 通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )
通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
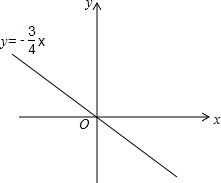 在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.
在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com