
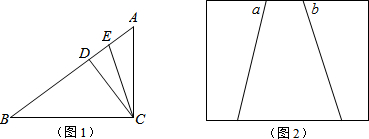
分析 (1)作EM⊥AC交AC于点M,利用勾股定理求出BC,再利用△ACD∽△ABC,得出$\frac{EM}{AE}$=$\frac{BC}{AB}$,可解得AD的值,由角平分线定理可得EM=DE,联立可解出AE的值,利用BE=AB-AE即可求解,
(2)延长两边分别作两组角的平分线,连接平分线的两个交点所在的线就是这个角的平分线.
解答 解:(1)如图1,作EM⊥AC交AC于点M,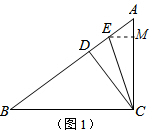
∵Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=5,AC=3,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵△ACD∽△ABC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即$\frac{AD}{3}$=$\frac{3}{5}$,解得AD=$\frac{9}{5}$,
∵∠ABC=∠AEM,
∴$\frac{EM}{AE}$=$\frac{BC}{AB}$,即$\frac{EM}{AE}$=$\frac{4}{5}$,
∵CE平分∠ACD,CD⊥AB,EM⊥AC,
∴EM=DE,
∴$\frac{DE}{AE}$=$\frac{4}{5}$且DE+AE=$\frac{9}{5}$,解得DE=$\frac{4}{5}$,AE=1,
∴BE=AB-AE=5-1=4.
(2)如图2,延长两边分别作两组角的平分线,连接平分线的两个交点所在的线就是这个角的平分线.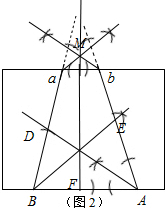
点评 本题主要考查了作图,角平分线的性质及勾股定理,解题的关键是理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:填空题
已知m+n=2,mn=-2,则(1-m)(1-n)=___________。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
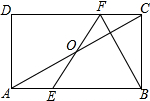 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com