
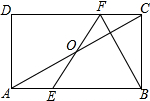
 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
分析 连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.
解答 解:如图,连接OB,
∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∴∠FCA=30°,
∴∠FBC=30°,
∵FC=2,
∴BC=$2\sqrt{3}$,
∴AC=2BC=4$\sqrt{3}$,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}=\sqrt{(4\sqrt{3})^{2}-(2\sqrt{3})^{2}}=6$,
故选D
点评 本题考查了矩形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形30°角所对的直角边等于斜边的一半,综合题,但难度不大,(2)作辅助线并求出∠BAC=30°是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
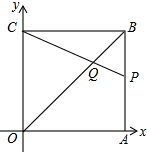 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
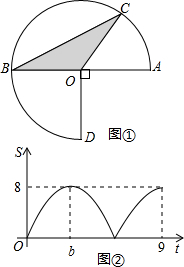 如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:
如图①,点C在以O为圆心,以AB为半径的圆弧上从A点开始以a度/秒的速度逆时针运动到点D,OD⊥AB.在此运动过程中,△BOC的面积S与运动时间t(秒)之间的函数图象(非抛物线)如图②所示,根据函数图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
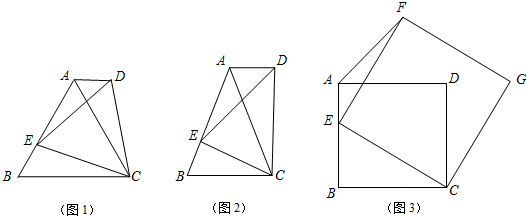
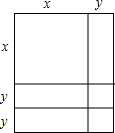 通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )
通过计算几何图形的面积可表示一些代数恒等式,小明从图中得到4个代数恒等式:①x(x+y)=x2+xy;②x2+3xy+2y2=(x+y)(x+2y);③(x+2y)2=x2+4xy+4y2;④x2+2xy+y2=(x+y)2.其中正确的有( )| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com