
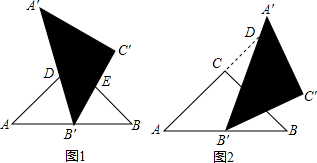
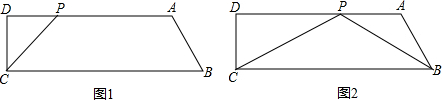
分析 (1)根据题意可知∠A=∠B=45°,然后根据∠ADB′+∠A=∠A′B′C′+∠EB′B,从而可证明:∠ADB′=∠EB′B,从而可证明两三角形相似;
(2)根据(1)的思路证明:∠A=∠B,∠ADB′=∠EB′B,从而可证明两三角形相似;
(3)由(2)可知△AB′D∽△BEB′,根据相似三角形的性质可知$\frac{AD}{BB′}=\frac{B′D}{EB′}$,因为BB′=AB′,从而可得到$\frac{AD}{AB′}=\frac{B′D}{B′E}$,又因为∠A=∠A′B′C′=45°,从而可证明△AB′D∽△B′ED;
(4)当∠A′B′C′=15°时,可证明∠ADB′=∠EB′B,∠A=∠B,从而可证明两三角形相似.
解答 证明:(1)由等腰直角三角形的性质可知:∠A=∠B=∠A′B′C′=45°,
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-45°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-45°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
(2)相似.
如下图: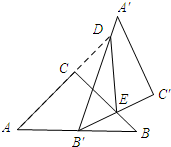
理由:由等腰直角三角形的性质可知:∠A=∠B=∠A′B′C′=45°,
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-45°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-45°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
(3)由(2)可知
∴△AB′D∽△BEB′,
∴$\frac{AD}{BB′}=\frac{B′D}{EB′}$,
又∵BB′=AB′,
∴$\frac{AD}{AB′}=\frac{B′D}{B′E}$,
又∵∠A=∠A′B′C′=45°.
∴△AB′D∽△B′ED.
(4)当∠A′B′C′=15°时,△AB′D∽△BEB′.
理由:∵∠C=150°,AC=BC,
∴∠A=∠B=15°.
∵∠BB′D=∠ADB′+∠A,∠BB′D=∠A′B′C′+∠EB′B,
∴∠ADB′=∠BB′D-∠A=∠BB′D-15°,∠EB′B=∠BB′D-∠A′B′C′=∠BB′D-15°.
∴∠ADB′=∠EB′B.
又∵∠A=∠B,
∴△AB′D∽△BEB′.
点评 本题主要考查的是相似三角形的性质和判定,利用三角形外角的性质和等腰三角形的性质证得∠ADB′=∠EB′B是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:单选题
图①,在边长为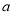 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为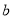 的小正方形(
的小正方形(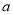 >
> 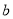 ),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )
),把余下部分剪拼成一个矩形(如图②),通过计算两个图形的面积,验证了一个等式,则这个等式是( )

A. (a+2b)(a-b)=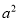 +ab-2
+ab-2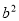
B. 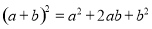
C. 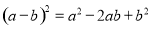
D. 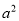 -
-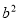 =(a+b)(a-b)
=(a+b)(a-b)
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
(2014山东莱芜)已知一次函数y=ax+b与反比例函数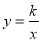 的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.
的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:选择题
为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
A.2500(1+x)2=1.2
B.2500(1+x)2=12000
C.2500+2500(1+x)+2500(1+x)2=1.2
D.2500+2500(1+x)+2500(1+x)2=12000
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
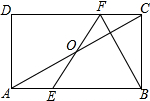 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com