
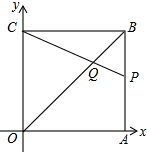
 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$). 分析 首先根据点Q在OB:y=x上,以及QO=OC=2,求出点Q的坐标是多少;然后设点P的坐标是(2,a),确定出CP所在的直线的解析式,再根据点Q在CP上,求出a的值,即可求出点P的坐标是多少.
解答 解:∵点Q在OB:y=x上,QO=OC=2,
∴点Q的坐标是($\sqrt{2}$,$\sqrt{2}$),
设P点的坐标是(2,a),
∵点C的坐标是(0,2)
∴CP所在的直线的解析式是:y=kx+2,
则k=(a-2)÷(2-0)=0.5a-1,
∴CP所在的直线的解析式是:y=(0.5a-1)x+2,
∵点Q($\sqrt{2}$,$\sqrt{2}$)在y=(0.5a-1)x+2上,
∴(0.5a-1)×$\sqrt{2}$+2=$\sqrt{2}$
则a=4-2$\sqrt{2}$,
∴点P的坐标为(2,4-2$\sqrt{2}$),
∴点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
故答案为:(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
点评 (1)此题主要考查了正方形的性质和应用,要熟练掌握,解答此题的关键是要明确:①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;③正方形具有四边形、平行四边形、矩形、菱形的一切性质.④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.
(2)此题还考查了一次函数图象上点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.
(3)此题还考查了待定系数法求一次函数解析式的方法,要熟练掌握.


科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
(2014山东莱芜)已知一次函数y=ax+b与反比例函数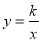 的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.
的图象相交于A(4,2)、B(-2,m)两点.则一次函数的表达式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
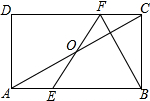 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
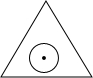 如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.
如图,一个半径为r的圆形纸片在边长为a(a≥2$\sqrt{3}$r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是$(3\sqrt{3}-π){r}^{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com