
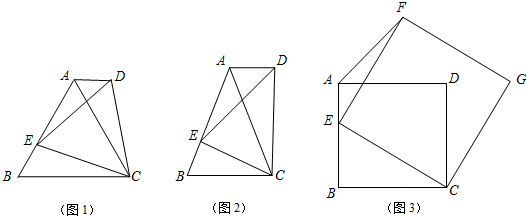
分析 (1)由等边三角形的性质可知:BC=AC,CE=CD,然后再证明∠BCE=∠ACD,从而可得到△BCE≌△ACD故此可知∠B=∠DAC;
(2)由于△ABC和△DEC都是等腰三角形,且△DEC∽△ABC,从而可证得:$\frac{DC}{CE}=\frac{AC}{BC}$,然后再证明∠DCA=∠ECB,所以△DCA∽△ECB,从而可证明∠DAC=∠ACB,由平行线的判定定理可知AD∥BC;
(3)①由正方形的性质可知BC=CD,CE=CG,∠BCD=∠ECG=90°,从而可证明△BCE≌△DCG 故此∠B=∠CDG=90°,由于∠ADC=90°,所以点G一定在AD的延长线上;②先证明∠BCE=∠FGH=∠GCD.从而可得到△FHG≌△GDC≌△EBC,然后再证明△AFH是等腰直角三角形,故此∠FAG=45°,所以点F的运动路径长=AC.
解答 解:(1)∠DAC=∠B
理由如下:
∵△ABC和△DEC都是等边三角形
∴∠DCE=∠ACB=60°
∴∠BCE=∠ACD
在△BEC和△ADC中,
$\left\{\begin{array}{l}{BC=AC\\;}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$
∴△BCE≌△ACD.
∴∠B=∠DAC.
(2)AD∥BC》
理由如下:
∵△ABC和△DEC都是等腰三角形,且△DEC∽△ABC
∴$\frac{DC}{CE}=\frac{AC}{BC}$
∵∠DCE=∠ACB,
∴∠DCA=∠ECB.
∴△DCA∽△ECB.
∴∠DAC=∠EBC=∠ACB.
∴AD∥BC.
(3)①连结DG.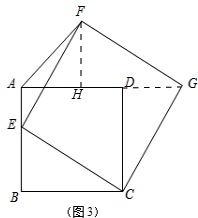
∵四边形ABCD和FECG都是正方形
∴BC=CD,CE=CG,∠BCD=∠ECG=90°.
∴∠BCE=∠DCG.
∴△BCE≌△DCG.
∴∠B=∠CDG=90°.
∵∠ADC=90°.
∴∠ADC+∠CDG=180°
∴点G一定在AD的延长线上.
②作FH⊥AG于点H.
∵∠BCE+ECD=90°,∠ECD+DCG=90°,
∴∠BCE=∠GCD.
∵∠GCD+∠CGD=90°,∠CGD+∠FGH=90°
∴∠FGH=∠GCD.
∴∠BCE=∠FGH=∠GCD.
在△FHG和△GDC和△EBC中,
$\left\{\begin{array}{l}{∠BCE=∠FGH=∠GCD}\\{∠EBC=∠CDG=∠FHG}\\{EC=CG=FG}\end{array}\right.$,
∴△FHG≌△GDC≌△EBC,
∴FH=BE=DG,HG=BC,
∴AH=AG-GH=AD+DG-GH=BC+DG-BC=DG=FH,
∴△AFH是等腰直角三角形,
∴∠FAG=45°.
∴点F的运动路径长=AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题主要考查的是等腰三角形的性质、等边三角形的性质、正方形的性质以及全等三角形的性质和判定,相似三角形的性质和判定,证得△DCA∽△ECB.
、△FHG≌△GDC≌△EBC是解题的关键.


科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:选择题
为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
A.2500(1+x)2=1.2
B.2500(1+x)2=12000
C.2500+2500(1+x)+2500(1+x)2=1.2
D.2500+2500(1+x)+2500(1+x)2=12000
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
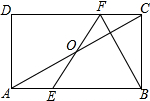 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )| A. | 8$\sqrt{3}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差是44 | B. | 众数是61 | C. | 平均数是62 | D. | 中位数是61 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com