
 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹.反弹时反射角等于入射角,当点P第2016次碰到矩形的边时,点P的坐标为( )| A. | (0,3) | B. | (5,0) | C. | (7,4) | D. | (8,3) |
分析 根据反弹时反射角等于入射角画出点的运动轨迹,表示出点的坐标,总结规律得到答案.
解答 解:如图,根据反射角与入射角的定义作出图形,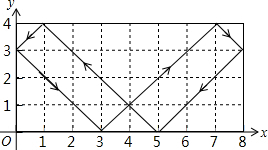
当点P第1次碰到矩形的边时,点P的坐标为(3,0),
当点P第2次碰到矩形的边时,点P的坐标为(7,4),
当点P第3次碰到矩形的边时,点P的坐标为(8,3),
当点P第4次碰到矩形的边时,点P的坐标为(5,0),
当点P第5次碰到矩形的边时,点P的坐标为(1,4),
当点P第6次碰到矩形的边时,点P的坐标为(0,3),
当点P第7次碰到矩形的边时,点P的坐标为(3,0),
∴每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(0,3),
∵2016÷6=336,
∴当点P第2016次碰到矩形的边时,点P的坐标为(0,3).
故选:A.
点评 本题考查的是根据图形找出点的坐标的变化规律,正确理解题意、画出合适的示意图、表示出变化过程中各点的坐标、正确总结规律是解题的关键.


科目:初中数学 来源: 题型:选择题
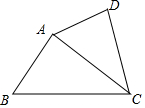 如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )| A. | ∠DAC=∠ABC | B. | AC是∠BCD的平分线 | ||
| C. | AC2=BC•CD | D. | $\frac{AD}{AB}$=$\frac{DC}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
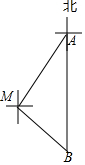 如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处
如图,一艘渔船位于小岛M的北偏东30°方向,距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛东南方向的B处查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com