
【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD是角平分线,DE⊥AB于E,AD、CE相交于点H,则图中的等腰三角形有( )
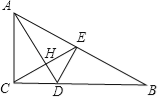
A. 2个 B. 3个 C. 4个 D. 5个
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】腰长为4的等腰直角![]() 放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90
放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90![]() ,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当
,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当![]() 时,以PB为直角边作等腰直角
时,以PB为直角边作等腰直角![]() ,则所有符合条件的点M的坐标为________.
,则所有符合条件的点M的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′,并使其面积为矩形ABCD面积的一半,若A′D′与CD交于点E,且AB=2,则△ECD′的面积是_____.
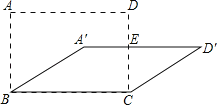
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形EGFH是矩形.
小明继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
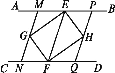
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____,MN∥EF,可得NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____,_____,故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)7x(3x-4)=9(3x-4);
(2)x2-6x+9=(5-2x)2;
(3)2x2-5x-7=0;
(4)x2-2x-1=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形顶点![]() 为
为![]() 轴正半轴上一点,点
轴正半轴上一点,点![]() 在第一象限,点
在第一象限,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() .动点
.动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),点
重合),点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() ,
,![]() ,设
,设![]() 的长为
的长为![]() .
.

(1)填空:线段![]() 的长=________,线段
的长=________,线段![]() 的长=________;
的长=________;
(2)求![]() 的长,并用含
的长,并用含![]() 的代数式表示.
的代数式表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com