
【题目】如图,已知![]() 是反比例函数
是反比例函数![]() 图象上的两点,
图象上的两点,![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从坐标原点
从坐标原点![]() 出发,沿
出发,沿![]() 匀速运动,终点为
匀速运动,终点为![]() .过点
.过点![]() 作
作![]() 轴于
轴于![]() .设
.设![]() 的面积为
的面积为![]() 点
点![]() 运动的时间为
运动的时间为![]() 则
则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )

A.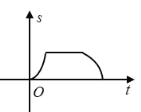 B.
B.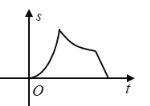
C. D.
D.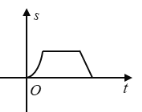
科目:初中数学 来源: 题型:
【题目】向阳村2017年的人均收入为30000元,2019年的人均收入为36300元.
(1)求2017年2019年该村人均收入的年平均增长率;
(2)假设2020年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2020年该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
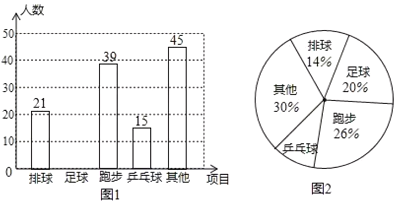
【题目】某校开展“我最喜欢的一项体育社团活动”调查,若每名学生必选且只能选一项,现随机抽查了![]() 名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
名学生,并将其结果绘制成如下不完整的统计图,请解答下列问题:
(1)求![]() 的值;
的值;
(2)补全条形统计图;
(3)求“乒乓球”所对应的扇形圆心角的度数;
(4)已知该校共有2400名学生,请你估计该校学生最喜欢篮球社团活动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位![]() ),右边为华氏温度的刻度和读数(单位
),右边为华氏温度的刻度和读数(单位![]() ).从温度计的刻度上可以看出,摄氏温度
).从温度计的刻度上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 部分对应关系如下表:
部分对应关系如下表:
| ··· |
|
| ··· |
| ··· |
|
| ··· |

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当摄氏温度为零下![]() 时,求华氏温度为多少?
时,求华氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
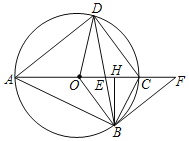
【题目】如图,四边形ABCD内接于⊙O,直径AC与弦BD的交点为E,OB∥CD,BH⊥AC,垂足为H,且∠BFA=∠DBC.
(1)求证:BF是⊙O的切线;
(2)若BH=3,求AD的长度;
(3)若sin∠DAC=![]() ,求△OBH的面积与四边形OBCD的面积之比.
,求△OBH的面积与四边形OBCD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春临大地,学校决定给长12米,宽9米的一块长方形展示区进行种植改造现将其划分成如图两个区域:区域Ⅰ矩形ABCD部分和区域Ⅱ四周环形部分,其中区域Ⅰ用甲、乙、丙三种花卉种植,且EF平分BD,G,H分别为AB,CD中点.
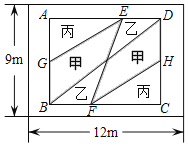
(1)若区域Ⅰ的面积为Sm2,种植均价为180元/m2,区域Ⅱ的草坪均价为40元/m2,且两区域的总价为16500元,求S的值.
(2)若AB:BC=4:5,区域Ⅱ左右两侧草坪环宽相等,均为上、下草坪环宽的2倍
①求AB,BC的长;
②若甲、丙单价和为360元/m2,乙、丙单价比为13:12,三种花卉单价均为20的整数倍.当矩形ABCD中花卉的种植总价为14520元时,求种植乙花卉的总价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com