
 ,则∠APB的度数是________.
,则∠APB的度数是________. ,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B=
,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B= ∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.
∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.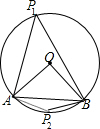
 ,
, ∠AOB=45°,
∠AOB=45°,

科目:初中数学 来源: 题型:
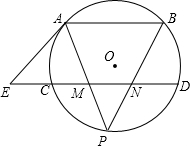 如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧 | CD |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年吉林镇赉胜利中学九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知OA、OB是⊙O的两条半径,且OA⊥BC,C为OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD,交OC过于点E。
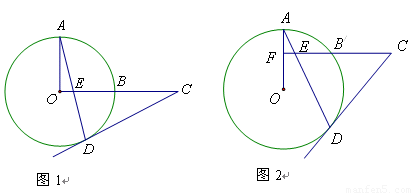
(1)求证:CD=CE;
(2)若将图1中的半径OB所在的直线向上平行移动,交⊙O于 ,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com