
情境·观察:
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△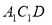 ,如图1所示,将△
,如图1所示,将△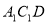 的顶点
的顶点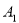 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A(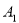 ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角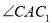 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。
问题·探究:
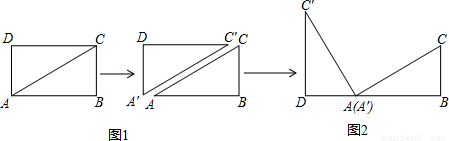
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。
关系·拓展:
如图4,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点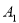 ,连接
,连接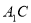 ,求
,求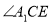 的度数。
的度数。
(1) 90°,AD;(2)EP=FQ,证明见解析;(3)45°.
【解析】
试题分析:(1)根据矩形的性质、旋转的性质填空;
(2)由全等三角形△APE≌△BGA的对应边相等知,EP=AG;同理由全等三角形△FQA≌△AGC的对应边相等知FQ=AG,所以易证EP=FQ;
(3)由旋转的性质易求∠A1CE=45°.
试题解析:(1)∵四边形ABCD是矩形,
∴如图1,在Rt△ADC与Rt△ABC中,
 ,
,
∴Rt△ADC≌Rt△ABC(HL),
即如图2,Rt△ABC≌Rt△C'DA′,
∴BC=AD,∠BAC=∠DC′A′.
又∵∠DC′A′+∠DA′C′=90°,
∴∠DA′C′+∠CAB=90°,
∴∠CAC′=90°.
问题·探究:
【解析】
EP=FQ
∵∠AGB=∠EPA=∠EAB=90°
∴∠EAP+∠PEA=90°
∠EAP+∠BAG=90°
∴∠BAG=∠PEA
∵∠EPA=∠AGB
∠PEA=∠BAG
AE=AB
∴△EPA≌△AGB
∴EP=AG
同理:QF=AG
∴EP=FQ
联系·拓展:
【解析】
∠A1CE=45°
过A1作A1Q⊥BE于点Q

由上可知:△ABP≌△A1QP
∴BP=A1Q,AB=PQ
∵AB=BC
∴BC=PQ
∴BP=CQ
∴A1Q=CQ
∴∠A1CE =45°
考点: 相似形综合题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源:2015届辽宁省北票市八年级下学期期中考试数学试卷(解析版) 题型:选择题
八年级(1)班共有40名学生,其中22名男同学.本学期经班委讨论决定向希望工程捐款,已知男同学平均每人捐款2.5元,如果要使班级平均每人捐款达到2.8元,那么女同学平均每人至少捐款(精确到0.0l元) ( )
A.3元 B.3.17元 C. 3.16元 D.3.15元
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省丹东市八年级下学期期中考试数学试卷(解析版) 题型:填空题
下列图形:①线段;②等边三角形;③平行四边形;④等腰梯形;⑤长方形;⑥圆。其中既是轴对称图形,又是中心对称图形的有 (填序号)
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省丹东市八年级下学期期中考试数学试卷(解析版) 题型:选择题
下列变形,是因式分解的是( )
A.x(x-1)=x2-x B.x2-x+1 = x(x-1)+1
C.x2-x = x(x-1) D.2a(b+c)=2ab+2ac
查看答案和解析>>
科目:初中数学 来源:2015届福建省福鼎市十校联合八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,∠A=∠D=90°,AC=BD,
(1)求证:AB=CD
(2)请判断△OBC的形状,并说明理由。

查看答案和解析>>
科目:初中数学 来源:2015届甘肃省八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点
(1)求证:△ABE≌△DCE
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与GH有什么数量关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2015届湖南长沙麓山国际实验学校八年级下学期期中数学试卷(解析版) 题型:选择题
若正比例函数y=kx的图象经过点(1,2),则k的值为( )
A.-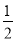 B.-2 C.
B.-2 C. D.2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com