
【题目】已知⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(![]() ,0),
,0),![]() CAB=90°, AC=AB,顶点A在⊙O上运动.
CAB=90°, AC=AB,顶点A在⊙O上运动.
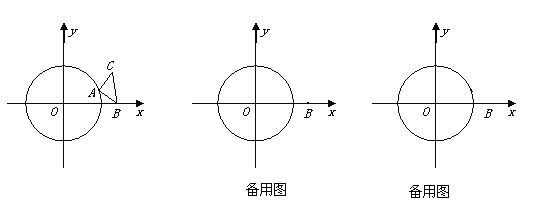
(1)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
【答案】(1)![]() ,其中-1≤x≤1,S的最大值为
,其中-1≤x≤1,S的最大值为![]() ,最小值为
,最小值为![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题(1)过点A作AE⊥OB于点E,在Rt△OAE中求AE的长,然后再在Rt△BAE中求出AB的长,进而求出面积的表达式,结合定义域,根据一次函数的性质确定最大最小值;
(2)相切时有两种情况,在第一象限或者第四象限,连接OA,并过点A作AE⊥OB于点E,在Rt△OAE中求出OE,然后就能求出A点坐标,AB所在直线对应的函数关系式很容易就能求出.
试题解析:(1)如图1,连接OA,过点A作AE⊥OB于点E,
在Rt△OAE中,![]() ,
,
在Rt△BAE中,![]() ,
,
∴![]() ,其中-1≤x≤1.
,其中-1≤x≤1.
∴当x=-1时,S的最大值为![]() ,当x=1时,S的最小值为
,当x=1时,S的最小值为![]() .
.
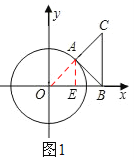
(2)①当点A位于第一象限时(如图1),连接OA,并过点A作AE⊥OB于点E,
∵直线AB与⊙O相切,∴∠OAB=90°.
又∵∠CAB=90°,∴∠CAB+∠OAB=180°.∴点O、A、C在同一条直线.
∴∠AOB=∠C=45°,即∠CBO=90°.
在Rt△OAE中,OE=AE=![]() ,点A的坐标为(
,点A的坐标为(![]() ,
,![]() ).
).
又∵B的坐标为(![]() ,0),∴过A、B两点的直线为
,0),∴过A、B两点的直线为![]() .
.
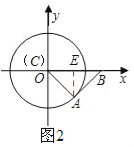
②当点A位于第四象限时(如图2),点A的坐标为(![]() ,
,![]() ),
),
∵B的坐标为(![]() ,0),∴过A、B两点的直线为
,0),∴过A、B两点的直线为![]() .
.
综上所述,过A、B两点的直线为![]() 或
或![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
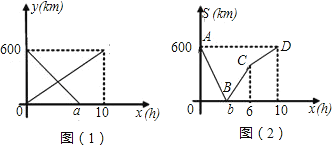
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地的距离为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为S(km),y1,y2与x的函数关系图象如图(1)所示,S与x的函数关系图象如图(2)所示:
(1)图中的a= ,b= .
(2)求S关于x的函数关系式.
(3)甲、乙两地间依次有E、F两个加油站,相距200km,若慢车进入E站加油时,快车恰好进入F站加油.求E加油站到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,与直线OC:
轴交于点B,与直线OC:![]() 交于点C.
交于点C.
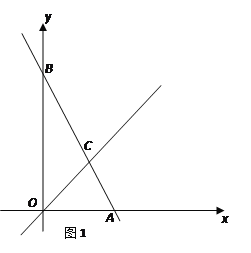

(1)若直线AB解析式为![]() ,
,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作![]() 的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.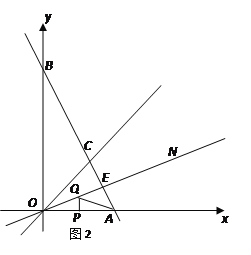
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的形统计图和不完整的条形统计图:
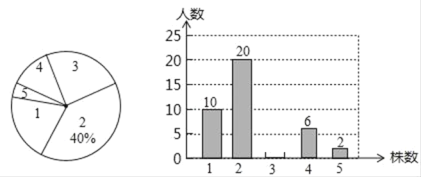
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)该班同学植树株数的中位数是 ;
(3)求该班同学平均植树的株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=![]() .
.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着电影《流浪地球》的热映,科幻大神刘慈欣的著作受到广大书迷的追捧,《流浪地球》《球状闪电》《三体》《超新星纪元》四部小说在某网上书城热销.已知《流浪地球》的销售单价与《球状闪电》相同,《三体》的销售单价是《超新星纪元》单价的3倍,《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;若自电影上映以来,《流浪地球》与《超新星纪元》的日销售量相同,《球状闪电》的日销售量为《三体》日销售量的3倍,《流浪地球》与《三体》的日销售量和为450本,且《流浪地球》的日销售量不低于《三体》的日销量的![]() 且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com