
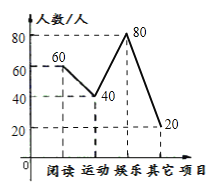
”¾ĢāÄæ”æijŠ£ĪŖŃŠ¾æѧɜµÄæĪÓą»ī¶ÆĒéæö£¬²ÉČ”³éŃłµÄ·½·Ø£¬“ÓŌĶĮ”¢ŌĖ¶Æ”¢ÓéĄÖ”¢ĘäĖüµČĖÄøö·½Ćęµ÷²éĮĖČōøÉĆūѧɜµÄŠĖȤ°®ŗĆ£¬²¢½«µ÷²éµÄ½į¹ū»ęÖĘĮĖČēĻĀµÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£ØČēĶ¼£©£¬ĒėÄćøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ


¢ŁÕā“Īµ÷ŃŠ£¬Ņ»¹²µ÷²éĮĖ ČĖ£®
¢ŚÓŠŌĶĮŠĖȤµÄŃ§ÉśÕ¼±»µ÷²éѧɜ×ÜŹżµÄ %£®
¢ŪÓŠ”°ĘäĖü”±°®ŗƵÄѧɜ¹²¶ąÉŁČĖ£æ
¢Ü²¹Č«ÕŪĻßĶ³¼ĘĶ¼£®
”¾“š°ø”æ¢Ł200£»¢Ś30%£»¢Ū20£»¢ÜĻź¼ū½āĪö
”¾½āĪö”æ
¢ŁÓÉÕŪĻßĶ³¼ĘĶ¼æÉŅŌ擳ö°®ŗĆŌĖ¶ÆµÄČĖŹżŹĒ40ČĖ£¬ÓÉÉČŠĪĶ³¼ĘĶ¼æ“³ö°®ŗĆŌĖ¶ÆµÄČĖŹżÕ¼³éŃłČĖŹżµÄ20%£¬øł¾Ż°Ł·ÖŹż³ż·ØµÄŅāŅ壬ÓĆ°®ŗĆŌĖ¶ÆµÄŹż³żŅŌĖłÕ¼µÄ°Ł·ÖĀŹ¾ĶŹĒ±»³éŃłµ÷²éµÄČĖŹż£»
¢ŚÓĆÓŠŌĶĮŠĖȤµÄѧɜŹż£Ø“ÓÕŪĻßĶ³¼ĘĶ¼æÉŅŌ擳ö£©³żŅŌ±»µ÷²é×ÜČĖŹż£Ø¢ŁŅŃĒó³ö£©£©£»
¢Ū°Ń±»µ÷²éµÄ×ÜČĖŹżæ“×÷µ„Ī»”°1”±£¬ÓĆ1¼õČ„ÓŠŌĶĮŠĖȤ”¢ŌĖ¶ÆŠĖȤ”¢ÓéĄÖŠĖȤČĖŹżĖłµÄ°Ł·ÖĀŹ¾ĶŹĒĘäĖüŠĖȤѧɜČĖŹżĖłÕ¼µÄ°Ł·ÖĀŹ£»øł¾Ż°Ł·ÖŹż³Ė·ØµÄŅāŅ壬ÓĆ×ÜČĖŹż³ĖĘäĖü°®ŗĆČĖŹżĖłÕ¼µÄ°Ł·ÖĀŹ¾ĶŹĒÓŠ”°ĘäĖü”±°®ŗƵÄѧɜČĖŹż£»
¢Üøł¾Ż°Ł·ÖŹż³Ė·ØµÄŅāŅ壬ÓĆ×ÜČĖŹż³Ė°®ŗĆÓéĄÖČĖŹżĖłÕ¼µÄ°Ł·ÖĀŹĒó³ö°®ŗĆÓéĄÖČĖŹż£¬¼“æɲ¹Č«ÕŪĻßĶ³¼ĘĶ¼£®
½ā£ŗ¢Ł40”Ā20%= 200 ČĖ£¬
¼“Õā“Īµ÷ŃŠ£¬Ņ»¹²µ÷²éĮĖ200ČĖ£¬
¹Ź“š°øĪŖ£ŗ200£»
¢Ś60”Ā200= 30 %
¼“ÓŠŌĶĮŠĖȤµÄŃ§ÉśÕ¼±»µ÷²éѧɜ×ÜŹżµÄ30%£¬
¹Ź“š°øĪŖ£ŗ30%£»
¢Ū1-20%-40%-30%=10%
200”Į10%=20£ØČĖ£©
¼“ÓŠ”°ĘäĖü”±°®ŗƵÄѧɜ¹²20ČĖ£¬
¹Ź“š°øĪŖ£ŗ20£»
¢Ü200”Į40%=80£ØČĖ£©
°®ŗĆÓéĄÖµÄ80ČĖ£¬”°ĘäĖü”±°®ŗƵÄ20ČĖ£¬²¹Č«ÕŪĻßĶ³¼ĘĶ¼ČēĻĀ£ŗ


 ×Ö“Ź¾äĘŖÓėĶ¬²½×÷ĪÄ“ļ±źĻµĮŠ“š°ø
×Ö“Ź¾äĘŖÓėĶ¬²½×÷ĪÄ“ļ±źĻµĮŠ“š°ø ×ß½ųĪÄŃŌĪÄĻµĮŠ“š°ø
×ß½ųĪÄŃŌĪÄĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ·½³ÉĶ¬Ń§æ“µ½Ņ»Ōņ²ÄĮĻ£ŗ¼×æŖĘū³µ£¬ŅŅĘļ×ŌŠŠ³µ“ÓMµŲ³ö·¢ŃŲŅ»Ģõ¹«Ā·ŌČĖŁĒ°ĶłNµŲ£®ÉčŅŅŠŠŹ»µÄŹ±¼äĪŖt£Øh£©£¬¼×ŅŅĮ½ČĖÖ®¼äµÄ¾ąĄėĪŖy£Økm£©£¬yÓėtµÄŗÆŹż¹ŲĻµČēĶ¼1ĖłŹ¾£®
·½³ÉĖ¼æ¼ŗó·¢ĻÖĮĖČēĶ¼1µÄ²æ·ÖÕżČ·ŠÅĻ¢£ŗŅŅĻČ³ö·¢1h£»¼×³ö·¢0.5Š”Ź±ÓėŅŅĻąÓö£®
ĒėÄć°ļÖś·½³ÉĶ¬Ń§½ā¾öŅŌĻĀĪŹĢā£ŗ
£Ø1£©·Ö±šĒó³öĻ߶ĪBC£¬CDĖłŌŚÖ±ĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©µ±20£¼y£¼30Ź±£¬ĒótµÄȔֵ·¶Ī§£»
£Ø3£©·Ö±šĒó³ö¼×£¬ŅŅŠŠŹ»µÄĀ·³ĢS¼×£¬SŅŅÓėŹ±¼ätµÄŗÆŹż±ķ“ļŹ½£¬²¢ŌŚĶ¼2ĖłøųµÄÖ±½Ē×ų±źĻµÖŠ·Ö±š»³öĖüĆĒµÄĶ¼Ļó£»
£Ø4£©±ūĘļĦĶŠ³µÓėŅŅĶ¬Ź±³ö·¢£¬“ÓNµŲŃŲĶ¬Ņ»¹«Ā·ŌČĖŁĒ°ĶłMµŲ£¬Čō±ū¾¹ż![]() hÓėŅŅĻąÓö£¬ĪŹ±ū³ö·¢ŗó¶ąÉŁŹ±¼äÓė¼×ĻąÓö£æ
hÓėŅŅĻąÓö£¬ĪŹ±ū³ö·¢ŗó¶ąÉŁŹ±¼äÓė¼×ĻąÓö£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AC=3£¬BC=4£¬AB=5£¬D”¢E·Ö±šŹĒ±ßAB”¢±ßBCÉĻµÄµć£¬°Ń”÷ABCŃŲ×ÅÖ±ĻßDE¶ŌÕŪ£¬¶„µćBµÄ¶ŌÓ¦µćŹĒµć![]() £®
£®
£Ø1£©ČēĶ¼1£¬Čē¹ūµć![]() ŗĶ¶„µćAÖŲŗĻ£¬ĒóCEµÄ³¤£»
ŗĶ¶„µćAÖŲŗĻ£¬ĒóCEµÄ³¤£»
£Ø2£©ČēĶ¼2£¬Čē¹ūµć![]() ĀäŌŚACµÄÖŠµć£¬ĒóCEµÄ³¤£®
ĀäŌŚACµÄÖŠµć£¬ĒóCEµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚćė“صŲÕšŹ®ÖÜÄź¼ĶÄīČÕ£¬Ä³½ĢÓż¼ÆĶŽųŠŠĮĖÖ÷Ģā¾čŹé»ī¶Æ£¬Ķ¬Ń§ĆĒČČĒéøßÕĒ£¬½ö½öĪåĢģ¾Ķ¾čŌłĶ¼ŹémĶņ²į£¬ĘäÖŠmÓė![]() »„ĪŖµ¹Źż£®“ĖŹ±½ĢÓż¼ÆĶžö¶Ø°ŃĖł¾čĶ¼Źé·ÖÅś“ĪŌĖĶłŹŠĒųÖܱߵĔ°Ļ£ĶūѧŠ£”±£¬¶ų¾čŹé»ī¶Æ½«ŌŁ³ÖŠųŅ»ÖÜ£®ĻĀ±ķĪŖ»ī¶Æ½įŹųĒ°Ņ»ÖÜĖł¾čĶ¼Źé“ęĮæµÄŌö¼õ±ä»ÆĒéæö£Øµ„Ī»£ŗĶņ²į£©£ŗ
»„ĪŖµ¹Źż£®“ĖŹ±½ĢÓż¼ÆĶžö¶Ø°ŃĖł¾čĶ¼Źé·ÖÅś“ĪŌĖĶłŹŠĒųÖܱߵĔ°Ļ£ĶūѧŠ£”±£¬¶ų¾čŹé»ī¶Æ½«ŌŁ³ÖŠųŅ»ÖÜ£®ĻĀ±ķĪŖ»ī¶Æ½įŹųĒ°Ņ»ÖÜĖł¾čĶ¼Źé“ęĮæµÄŌö¼õ±ä»ÆĒéæö£Øµ„Ī»£ŗĶņ²į£©£ŗ
µŚŅ»Ģģ | µŚ¶žĢģ | µŚČżĢģ | µŚĖÄĢģ | µŚĪåĢģ | µŚĮłĢģ | µŚĘßĢģ |
+0.2 | +0.1 | ©0.1 | ©0.4 | +0.3 | +0.5 | ©0.1 |
£Ø1£©mµÄÖµĪŖ”” ””£®
£Ø2£©Ēó»ī¶Æ½įŹųŹ±£¬øĆ½ĢÓż¼ÆĶÅĖł¾čĶ¼Źé“ęĮæĪŖ¶ąÉŁĶņ²į£»
£Ø3£©»ī¶Æ½įŹųŗó£¬øĆ½ĢÓż¼ÆĶžö¶ØŌŚ6ĢģÄŚ°ŃĖł¾čĶ¼ŹéČ«²æŌĖĶł”°Ļ£ĶūѧŠ£”±£¬ĻÖÓŠA”¢BĮ½øöŌĖŹä¹«Ė¾£¬BŌĖŹä¹«Ė¾ĆæĢģµÄŌĖŹäŹżĮæŹĒAŌĖŹä¹«Ė¾µÄ1.5±¶£¬Ń§Š£Ź×ĻČĘøĒėAŌĖŹä¹«Ė¾½ųŠŠŌĖŹä£¬¹¤×÷Į½Ģģŗó£¬ÓÉÓŚÄ³Š©ŌŅņ£¬AŌĖŹä¹«Ė¾ĆæĢģŌĖŹäµÄŹżĮæ±ČŌĄ“½µµĶĮĖ25%£¬Ń§Š£¾ö¶ØÓÖĘøĒėBŌĖŹä¹«Ė¾¼ÓČė£¬ÓėAŌĖŹä¹«Ė¾¹²Ķ¬ŌĖŹä£¬Ē”ŗĆ°“Ź±Ķź³ÉČĪĪń£¬ĒóAŌĖŹä¹«Ė¾ĆæĢģŌĖŹä¶ąÉŁĶņ²įĶ¼Źé£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AC=BC£¬”ĻACB=90”ć£¬µćDŌŚBCÉĻ£¬BD=6£¬DC=2£¬µćPŹĒABÉĻµÄ¶Æµć£¬ŌņPC+PDµÄ×īŠ”ÖµĪŖ£Ø””””£©

A.8B.10C.12D.14
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĆęµÄ²ÄĮĻ£ŗ
Čē¹ūŗÆŹży£½f(x)Āś×ć£ŗ¶ŌÓŚ×Ō±äĮæxµÄȔֵ·¶Ī§ÄŚµÄČĪŅāx1£¬x2£¬
£Ø1£©Čō![]() £¬¶¼ÓŠ
£¬¶¼ÓŠ![]() £¬Ōņ³Ęf(x)ŹĒŌöŗÆŹż£»
£¬Ōņ³Ęf(x)ŹĒŌöŗÆŹż£»
£Ø2£©Čō![]() £¬¶¼ÓŠ
£¬¶¼ÓŠ![]() £¬Ōņ³Ęf(x)ŹĒ¼õŗÆŹż£®
£¬Ōņ³Ęf(x)ŹĒ¼õŗÆŹż£®
ĄżĢā£ŗÖ¤Ć÷ŗÆŹżf(x)£½![]() ŹĒ¼õŗÆŹż£®
ŹĒ¼õŗÆŹż£®
Ö¤Ć÷£ŗÉč![]() £¬
£¬
![]()
”ß![]() £¬
£¬
”ą![]() £®
£®
”ą![]() £®¼“
£®¼“![]() £®
£®
”ą![]() £®
£®
”ąŗÆŹż![]() ŹĒ¼õŗÆŹż£®
ŹĒ¼õŗÆŹż£®
øł¾ŻŅŌÉĻ²ÄĮĻ£¬½ā“šĻĀĆęµÄĪŹĢā£ŗ
ŅŃÖŖŗÆŹżf(x)£½![]() £Øx£¼0£©£¬ĄżČēf(£1)£½
£Øx£¼0£©£¬ĄżČēf(£1)£½![]() £½£3£¬f(£2)£½
£½£3£¬f(£2)£½![]() £½£
£½£![]()
£Ø1£©¼ĘĖć£ŗf(£3)£½ £»
£Ø2£©²ĀĻė£ŗŗÆŹżf(x)£½![]() £Øx£¼0£©ŹĒ ŗÆŹż£ØĢī”°Ōö”±»ņ”°¼õ”±£©£»
£Øx£¼0£©ŹĒ ŗÆŹż£ØĢī”°Ōö”±»ņ”°¼õ”±£©£»
£Ø3£©Ēė·ĀÕÕĄżĢāÖ¤Ć÷ÄćµÄ²ĀĻė£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ»ī¶ÆæĪÉĻ£¬Š”Ć÷ŗĶŠ”ŗģŗĻ×÷ÓĆŅ»ø±Čż½Ē°åĄ“²āĮæѧŠ£ĘģøĖøß¶Č£®ŅŃÖŖŠ”Ć÷µÄŃŪ¾¦ÓėµŲĆęµÄ¾ąĄė£ØAB£©ŹĒ1.7m£¬Ėūµ÷Õū×Ō¼ŗµÄĪ»ÖĆ£¬Éč·ØŹ¹µĆČż½Ē°åµÄŅ»ĢõÖ±½Ē±ß±£³ÖĖ®Ę½£¬ĒŅŠ±±ßÓėĘģøĖ¶„¶ĖMŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬²āµĆĘģøĖ¶„¶ĖMŃö½ĒĪŖ45”ć£»Š”ŗģµÄŃŪ¾¦ÓėµŲĆęµÄ¾ąĄė£ØCD£©ŹĒ1.5m£¬ÓĆĶ¬ŃłµÄ·½·Ø²āµĆĘģøĖ¶„¶ĖMµÄŃö½ĒĪŖ30”ć£®Į½ČĖĻą¾ą28Ć×ĒŅĪ»ÓŚĘģøĖĮ½²ą£ØµćB”¢N”¢DŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£©£®Ēó³öĘģøĖMNµÄøß¶Č£®£Ø²Īæ¼Źż¾Ż£ŗ ![]() £¬½į¹ū±£ĮōÕūŹż£®£©
£¬½į¹ū±£ĮōÕūŹż£®£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆŅ»Ģõ³¤ĪŖ18cmµÄĻøÉžĪ§³ÉŅ»øöµČŃüČż½ĒŠĪ.
£Ø1£©Čē¹ūŃü³¤ŹĒµ×±ß³¤µÄ2±¶£¬ĒóČż½ĒŠĪø÷±ßµÄ³¤£»
£Ø2£©ÄÜĪ§³ÉÓŠŅ»±ßµÄ³¤ŹĒ4cmµÄµČŃüČż½ĒŠĪĀš£æČōÄÜ£¬Ēó³öĘäĖūĮ½±ßµÄ³¤£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŹĢāĒé¾°£ŗČēĶ¼1£¬![]() ÖŠ£¬ÓŠŅ»æéÖ±½ĒČż½Ē°å
ÖŠ£¬ÓŠŅ»æéÖ±½ĒČż½Ē°å![]() ·ÅÖĆŌŚ
·ÅÖĆŌŚ![]() ÉĻ£Ø
ÉĻ£Ø![]() µćŌŚ
µćŌŚ![]() ÄŚ£©£¬Ź¹Čż½Ē°å
ÄŚ£©£¬Ź¹Čż½Ē°å![]() µÄĮ½ĢõÖ±½Ē±ß
µÄĮ½ĢõÖ±½Ē±ß![]() ”¢
”¢![]() Ē”ŗĆ·Ö±š¾¹żµć
Ē”ŗĆ·Ö±š¾¹żµć![]() ŗĶµć
ŗĶµć![]() .
.
ŹŌĪŹ![]() Óė
Óė![]() ŹĒ·ń“ęŌŚÄ³ÖÖČ·¶ØµÄŹżĮæ¹ŲĻµ£æ
ŹĒ·ń“ęŌŚÄ³ÖÖČ·¶ØµÄŹżĮæ¹ŲĻµ£æ
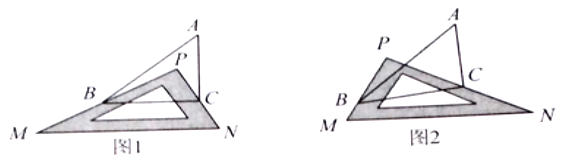
£Ø1£©ĢŲŹāŃŠ¾æ£ŗČō![]() £¬Ōņ
£¬Ōņ![]() ¶Č£¬
¶Č£¬![]() ¶Č£¬
¶Č£¬![]() ¶Č£»
¶Č£»
£Ø2£©Ąą±ČĢ½Ė÷£ŗĒėĢ½¾æ![]() Óė
Óė![]() µÄ¹ŲĻµ.
µÄ¹ŲĻµ.
£Ø3£©Ąą±ČŃÓÉģ£ŗČēĶ¼2£¬øıäÖ±½ĒČż½Ē°ü![]() µÄĪ»ÖĆ£»Ź¹
µÄĪ»ÖĆ£»Ź¹![]() µćŌŚ
µćŌŚ![]() Ķā£¬Čż½Ē°å
Ķā£¬Čż½Ē°å![]() µÄĮ½ĢõÖ±½Ē±ß
µÄĮ½ĢõÖ±½Ē±ß![]() ”¢
”¢![]() ČŌČ»·Ö±š¾¹żµć
ČŌČ»·Ö±š¾¹żµć![]() ŗĶµć
ŗĶµć![]() £¬£Ø2£©ÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£æČō²»³ÉĮ¢ĒėÖ±½ÓŠ“³öÄćµÄ½įĀŪ.
£¬£Ø2£©ÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£æČō²»³ÉĮ¢ĒėÖ±½ÓŠ“³öÄćµÄ½įĀŪ.
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com