Question

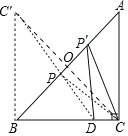
【题目】如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=6，DC=2，点P是AB上的动点，则PC+PD的最小值为（　　）

A.8B.10C.12D.14

Answer 1

【答案】B

【解析】

过点C作CO⊥AB于O，延长CO到C′，使OC′＝OC，连接DC′，交AB于P，连接CP，此时DP＋CP＝DP＋PC′＝DC′的值最小．由DC＝2，BD＝6，得到BC＝8，连接BC′，由对称性可知∠C′BA＝∠CBA＝45°，于是得到∠CBC′＝90°，然后根据勾股定理即可得到结论．

解：过点C作CO⊥AB于O，延长CO到C′，使OC′＝OC，连接DC′，交AB于P，连接CP．

此时DP＋CP＝DP＋PC′＝DC′的值最小．

∵DC＝2，BD＝6，

∴BC＝8，

连接BC′，由对称性可知∠C′BA＝∠CBA＝45°，

∴∠CBC′＝90°，

∴BC′⊥BC，∠BCC′＝∠BC′C＝45°，

∴BC＝BC′＝8，

根据勾股定理可得DC′＝．

故选：B．