
【题目】已知:如图,一次函数y=![]() x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
x+3的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.

(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,求点Q的坐标;若不存在,请说明理由.
【答案】(1)y=3x﹣6;(2)①Q的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,2);②点Q的坐标为(3,3)或(
,2);②点Q的坐标为(3,3)或(![]() ,
,![]() ).
).
【解析】
(1)求出C、D两点坐标即可解决问题;
(2)①分两种情形S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE分别构建方程即可;
S△BDE分别构建方程即可;
②分两种情形当:点D落在x正半轴上(记为点D1)时,如图2中.当点D落在y负半轴上(记为点D2)时,如图3中.分别求解即可
解:(1)由题意:D(4,6),C(2,0),
设直线CD的解析式为y=kx+b,则有![]() ,
,
解得![]() ,
,
∴直线CD的解析式为y=3x﹣6.
故答案为y=3x﹣6.
(2)①∵直线BQ将△BDE的面积分为1:2两部分,
∴S△BEQ=![]() S△BDE或S△BEQ=
S△BDE或S△BEQ=![]() S△BDE.
S△BDE.
在y=![]() x+3中,当x=0时,y=3;当x=4时,y=6.
x+3中,当x=0时,y=3;当x=4时,y=6.
∴B(0,3),D(4,6).
在y=3x﹣6中,当x=0时,y=﹣6.
∴E(0,﹣6).
∴BE=9.
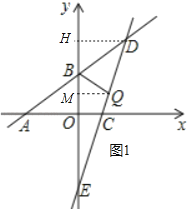
如图1中,过点D作DH⊥y轴于点H,则DH=4.
∴S△BDE=![]() BEDH=
BEDH=![]() ×9×4=18.
×9×4=18.
∴S△BEQ=![]() ×18=6或S△BEQ=
×18=6或S△BEQ=![]() ×18=12.
×18=12.
设Q(t,3t﹣6),由题意知t>0.
过点Q作QM⊥y轴于点M,则QM=t.
∴![]() ×9×t=6或
×9×t=6或![]() ×9×t=12.
×9×t=12.
解得t=![]() 或
或![]() .
.
当t=![]() 时,3t﹣6=﹣2;当t=
时,3t﹣6=﹣2;当t=![]() 时3t﹣6=2.
时3t﹣6=2.
∴Q的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,2).
,2).
②当点D落在x正半轴上(记为点D1)时,如图2中.
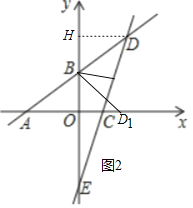
由(2)知B(0,3),D(4,6),
∴BH=BO=3.
由翻折得BD=BD1.
在△Rt△DHB和Rt△D1OB中,
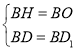 ,
,
∴Rt△DHB≌Rt△D1OB.
∴∠DBH=∠D1BO.
由翻折得∠DBQ=∠D1BQ.
∴∠HBQ=∠OBQ=90°.
∴BQ∥x轴.
∴点Q的纵坐标为3.
在y=3x﹣6中,当y=3时,x=3.
∴Q(3,3),
当点D落在y负半轴上(记为点D2)时,如图3中.
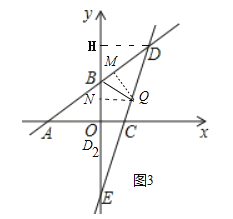
过点Q作QM⊥BD,QN⊥OB,垂足分别为点M、N.
由翻折得∠DBQ=∠D2BQ.
∴QM=QN.
由(2)知S△BDE=18,即S△BQD+S△BQE=18.
∴![]() BDQM+
BDQM+![]() BEQN=18.
BEQN=18.
在Rt△BDH中,由勾股定理,得BD=![]() =
=![]() =5.
=5.
∴![]() ×5QN+
×5QN+![]() ×9QN=18.
×9QN=18.
解得QN=![]() .
.
∴点Q的横坐标为![]() .
.
在y=3x﹣6中,当x=![]() 时,y=
时,y=![]() .
.
∴Q(![]() ,
,![]() ).
).
综合知,点Q的坐标为(3,3)或(![]() ,
,![]() ).
).
故答案为:(1)y=3x﹣6;(2)①Q的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,2);②点Q的坐标为(3,3)或(
,2);②点Q的坐标为(3,3)或(![]() ,
,![]() ).
).


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
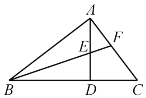
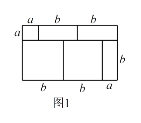
(2).阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到 ![]() .请解答下列问题:
.请解答下列问题:
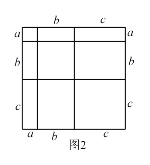
①.写出图2中所表示的数学等式;
②.利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
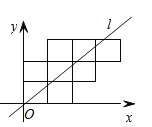
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
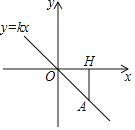
(1)求正比例函数的表达式;
(2)在x轴上能否找到一点M,使△AOM是等腰三角形?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
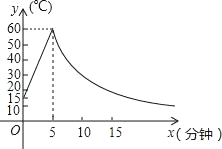
【题目】如图为某种材料温度y(℃)随时间x(min)变化的函数图象.已知该材料初始温度为15℃,温度上升阶段y与时间x成一次函数关系,且在第5分钟温度达到最大值60℃后开始下降;温度下降阶段,温度y与时间x成反比例关系.
(1)分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(2)根据工艺要求,当材料的温度高于30℃时,可以进行产品加工,问可加工多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
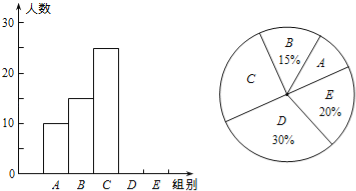
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com