
����Ŀ����ͼ����֪������![]() ��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1��
��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1��
��1����������ߵĽ���ʽ�Լ���B�����꣮
��2������M�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x���������˶���ͬʱ����N�ӵ�O��������ÿ��3����λ���ȵ��ٶ���y���������˶�����N�㵽��A��ʱ��M��Nͬʱֹͣ�˶���������M��x��Ĵ��߽��߶�AB�ڵ�Q�����������ڵ�P�����˶���ʱ��Ϊt�룮
����tΪ��ֵʱ���ı���OMPNΪ���Σ�
����t��0ʱ����BOQ�ܷ�Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
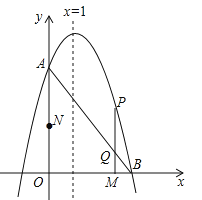
���𰸡���1��![]() ��B������Ϊ��3��0������2����������
��B��������3��0������2����������
��������
�����������1���ɶԳ��ṫʽ�����b����A����������c�������������߽���ʽ������y=0�����B�����ꣻ
��2������t�ɱ�ʾ��ON��OM����ɱ�ʾ��P�����꣬���ɱ�ʾ��PM�ij����ɾ��ε����ʿɵ�ON=PM���ɵõ�����t�ķ��̣������t��ֵ�����������֪OB=OA���ʵ���BOQΪ����������ʱ��ֻ����OB=BQ��OQ=BQ����t�ɱ�ʾ��Q������꣬��ɱ�ʾ��OQ��BQ�ij����ֱ�õ�����t�ķ��̣������t��ֵ��
���������
��1����������![]() �Գ�����ֱ��x=1������
�Գ�����ֱ��x=1������![]() =1�����b=2���������߹�A��0��3������c=3���������߽���ʽΪ
=1�����b=2���������߹�A��0��3������c=3���������߽���ʽΪ![]() ����y=0�ɵ�
����y=0�ɵ�![]() �����x=��1��x=3����B������Ϊ��3��0����
�����x=��1��x=3����B��������3��0����
��2�����������֪ON=3t��OM=2t����P���������ϣ���P��2t��![]() �������ı���OMPNΪ���Σ���ON=PM����3t=
�������ı���OMPNΪ���Σ���ON=PM����3t=![]() �����t=1��t=��
�����t=1��t=��![]() ����ȥ��������t��ֵΪ1ʱ���ı���OMPNΪ���Σ�
����ȥ��������t��ֵΪ1ʱ���ı���OMPNΪ���Σ�
�ڡ�A��0��3����B��3��0������OA=OB=3���ҿ����ֱ��AB����ʽΪy=��x+3������t��0ʱ��OQ��OB��������BOQΪ����������ʱ����OB=QB��OQ=BQ����������������֪OM=2t����Q��2t����2t+3������OQ=![]() =
=![]() ��BQ=
��BQ=![]() =
=![]() |2t��3|�����������֪0��t��1����OB=QBʱ������
|2t��3|�����������֪0��t��1����OB=QBʱ������![]() |2t��3|=3�����t=
|2t��3|=3�����t=![]() ����ȥ����t=
����ȥ����t=![]() ��
��
��OQ=BQʱ������![]() =
=![]() |2t��3|�����t=
|2t��3|�����t=![]() ��
��
���Ͽ�֪��t��ֵΪ![]() ��
��![]() ʱ����BOQΪ���������Σ�
ʱ����BOQΪ���������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����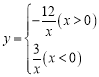 ��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2��
������P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ�
�����۵�P��ʲôλ�ã�ʼ����S��AOB=7.5��AP=4BP��
������P�ƶ���ʹ��AOB=90��ʱ����A������Ϊ��![]() ��
��![]() ����
����
������ȷ�Ľ��۸���Ϊ�� ��
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��y=3x��y������ƽ��3����λ���ֱ������Ӧ�ĺ�������ʽ��________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ���й����������������һ��ʡ�����к������ԼΪ2000000ƽ���������2000000�ÿ�ѧ��������ʾΪ2��10n �� ��n��ֵΪ�� ��
A.5
B.6
C.7
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=- ![]() x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���߶�AB���е�ΪD��3��2��������AOB��ֱ��CD�۵���ʹ��A���B�غϣ�ֱ��CD��x�ύ�ڵ�C��
x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���߶�AB���е�ΪD��3��2��������AOB��ֱ��CD�۵���ʹ��A���B�غϣ�ֱ��CD��x�ύ�ڵ�C��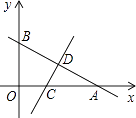
��1�����һ�κ����Ľ���ʽ��
��2�����C�����ꣻ
��3��������ƽ���ڴ��ڵ�P������C�⣩��ʹ����A��D��PΪ��������������ACDȫ�ȣ���ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬��B=30�㣬ADƽ�֡�CAB��DE��AB�ڵ�E������CE��AD�ڵ�H����ͼ�еĵ����������У� ��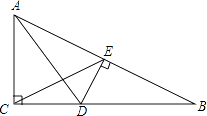
A.5��
B.4��
C.3��
D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��е�����¼��ǣ� ��
A. ̫���Ӷ������� B. С���ﳵ����ij��ʮ��·��ʱ�������
C. �ڱ�����ѹ�£��¶ȵ���0��ʱ���ڻ� D. ��յ�������2��31��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com