
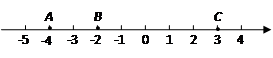
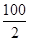 ,
,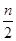
 -(2n-1),
-(2n-1), 时,|x-2︱+|x+3|=x-2+x+3=2x+1
时,|x-2︱+|x+3|=x-2+x+3=2x+1
 时,|x-2︱+|x+3|=2-x+x+3=5
时,|x-2︱+|x+3|=2-x+x+3=5

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
| A.(a+1)2的值是正数 | B.-(a+1)2的值是负数 |
| C.a2+1的值是正数 | D.-a2+1的值小于1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.-5+(-2) | B.-5-(-2) | C.|-5+(-2)| | D.|-2-(-5)| |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
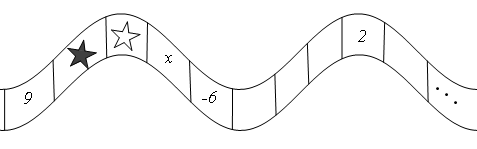
 ,第
,第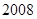 个格子中的数为__________;
个格子中的数为__________;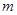 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为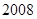 ?若能,求出
?若能,求出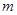 的值;若不能,请说明理由;
的值;若不能,请说明理由;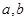 为前三个格子中的任意两个数,那么所有的
为前三个格子中的任意两个数,那么所有的 的和可以通过计算|
的和可以通过计算| ★|+|
★|+| ☆|+|★
☆|+|★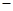 ☆|+|★
☆|+|★ |+|☆
|+|☆ |+|☆
|+|☆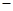 ★|得到,若
★|得到,若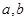 为前
为前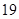 个格子中的任意两个数,则所有的
个格子中的任意两个数,则所有的 的和为__________.
的和为__________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com