
【题目】如果![]() 的乘积不含
的乘积不含![]() 和
和![]() 项,那么
项,那么![]() 和
和![]() 值分别是( )
值分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
先把(a2+pa+8)(a2-3a+q)按多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加展开,再根据乘积不含a3和a2项,列出-3a3+pa3=0,a2q-3a2p+8a2=0,再求解就容易了.
解:(a2+pa+8)(a2-3a+q)=a4-3a3+a2q+pa3-3a2p+pqa+8a2-24a+8q=a4+(-3a3+pa3)+(a2q-3a2p+8a2)+pqa-24a+8q,
∵(a2+pa+8)(a2-3a+q)的乘积不含a3和a2项,
∴-3a3+pa3=0,a2q-3a2p+8a2=0,
∴a3(-3+p)=0,a2(q-3p+8)=0,
∴-3+p=0,q-3p+8=0,
∴p=3,q=1.
故选:D.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
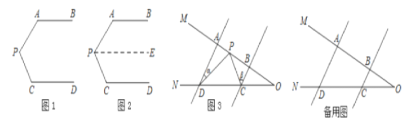
(1)天天同学看过图形后立即口答出:∠APC=110°,请你补全他的推理依据.
如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(___)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(___)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(___)
问题迁移:
(2)如图3,AD∥BC,当点P在A. B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由。
(3)在(2)的条件下,如果点P在A. B两点外侧运动时(点P与点A. B. O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图①'在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD= °;当∠BAP=α°(0<α<45°)时,则∠AFD= °;猜想线段DF, EF, AF之间的数量关系:DF-EF= AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD= °;线段DF, EF, AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD= °;请直接写出线段DF,EF,AF之间的数量关系: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 ▲ 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.

(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
材料一:对于任意的非零实数![]() 和正实数
和正实数![]() ,如果满足
,如果满足![]() 为整数,则称k是x的一个整商系数,
为整数,则称k是x的一个整商系数,
例如:当![]() 时,
时,![]() ,则称
,则称![]() 是
是![]() 的一个整商系数;
的一个整商系数;
当![]() 时,
时,![]() ,则称
,则称![]() 是
是![]() 的一个整商系数;
的一个整商系数;
当![]() 时,
时,![]() ,则称
,则称![]() 是
是![]() 的一个整商系数;
的一个整商系数;
给论:一个非零实数![]() 有无数个整商系数
有无数个整商系数![]() ,其中最小的一个整商系数记为
,其中最小的一个整商系数记为![]() ;
;
例如: ![]() ,
,
材料二:对于一元二次方程![]() 的两根
的两根![]() ,有如下关系:
,有如下关系:
![]()
请根据材料解决下列问题
![]()
![]()
![]() 若关于
若关于![]() 的方程:
的方程:![]() ,且满足
,且满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ;把
;把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() .依次类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点
.依次类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com