
【题目】(1)操作发现:
如图①'在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD= °;当∠BAP=α°(0<α<45°)时,则∠AFD= °;猜想线段DF, EF, AF之间的数量关系:DF-EF= AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD= °;线段DF, EF, AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD= °;请直接写出线段DF,EF,AF之间的数量关系: .

【答案】(1)45,45, ![]()
(2)30,改变,DF-EF=![]() AF
AF
(3)(90-![]() ),DF-EF=2sin
),DF-EF=2sin![]() ·AF
·AF
【解析】试题分析:对于(1),作AM垂直DE,在DF上取点G,使∠FAG=∠BAD=90°,根据B的对称点为E,四边形ABCD为正方形,即可求得△EAF≌△DAG,从而得出△AFG为等腰直角三角形,即可求出∠AFG,根据DF-EF=FG,在直角三角形FAG中,利用三角函数值,即可求得答案;
对于(2),作AM垂直DE,在DF上取点G,使∠FAG=∠BAD=120°,根据B的对称点为E,四边形ABCD为菱形,即可求得△EAF≌△DAG,从而得出△AFG为等腰直角三角形,即可求出∠AFG,根据DF-EF=FG,解直角三角形AFM,利用三角函数值求出FM=![]() AF,再根据FG=2FM,即可解答;
AF,再根据FG=2FM,即可解答;
对于(3),同理可证△EAF≌△DAG,从而得出△AFG为等腰直角三角形,即可求出∠AFG,解直角三角形AFM,利用三角函数值求出FM=sin![]() AF,即可解答.
AF,即可解答.
试题解析:(1)45°;45°;![]() .
.
(2)30°;DF,EF,AF间的数量关系发生变化,变为DF-EF=![]() AF.
AF.
理由如下:如图,在DF上取点G,使∠FAG=∠BAD=120°.

∵∠AFG=30°,
∴∠AGF=30°.
∴AF=AG.
由对称知AE=AB,
∠BAF=∠EAF,由菱形性质知AB=AD,
∴AE=AD,∠EAF=∠FAG-∠BAG=∠BAD-∠BAG=∠GAD.
∴△EAF≌△DAG,
∴EF=DG,
∴DF-EF=DF-DG=FG,
作AM⊥ED于M,
∵AF=AG,
∴FG=2FM,
在Rt△AFM中,
∠AFM=30°,∠AMF=90°,
∴FM=![]() AF.
AF.
∴DF-EF=FG=2FM=![]() AF.
AF.
(3)90°-![]() ;DF-EF=2sin
;DF-EF=2sin![]() AF.
AF.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】下列长度的各组线段能组成一个三角形的是( ).
A. 4cm,6cm,11cm B. 4cm,5cm,1cm
C. 3cm,4cm,5cm D. 2cm,3cm,6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
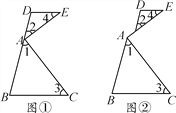
【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一粒米的质量约是0.0000021 kg,将数据0.0000021用科学记数法表示为( )
A. 21×10-5B. 2.1×10-7C. 2.1×10-5D. 2.1×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
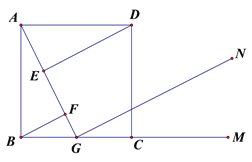
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽取了20个测量其直径,进行数据处理后,发现三组数据的平均数都是60mm,它们的方差依次为S甲2=0.612,S乙2=0.058,S丙2=0.149,根据以上提供的信息,你认为生产螺丝的质量最好的是__机床.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com