练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】侧面可以展开成一长方形的几何体有；圆锥的侧面展开后是一个；各个面都是长方形的几何体是；

    【答案】圆柱和棱柱；扇形；长方体
    【解析】柱体的侧面展开图是长方形，柱体包括圆柱和棱柱。圆锥的侧面展开后是一个扇形，其底面是一个圆。在柱体中，各个面都是长方形的几何体只有长方体，其他棱柱题展开后，除了侧面是长方形外，上下两底面有可能是圆、三角形、或其他多边形。
    【考点精析】认真审题，首先需要了解几何体的展开图(沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个边长为4cm的正方形折叠围成一个四棱柱的侧面，若该四棱柱的底面是一个正方形，则此正方形边长为cm.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面两个多位数1248624…… ，6248624…… ，都是按照如下方法得到的：将第一位数字乘以2，若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位．对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是（ ）

    A. 495 B. 497 C. 501 D. 503

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个多边形的内角和是外角和的2倍，此多边形是________边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝(x+4)2﹣3可以由抛物线y＝x2平移得到，则下列平移过程正确的是(　　)

    A.先向左平移4个单位，再向上平移3个单位

    B.先向左平移4个单位，再向下平移3个单位

    C.先向右平移4个单位，再向下平移3个单位

    D.先向右平移4个单位，再向上平移3个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC的边长为30，点M为线段AB上一动点，将等边△ABC沿过点M的直线折叠，使点A落在直线BC上的点D处，且BD∶DC＝1∶4，折痕与直线AC交于点N，则AN的长为________．

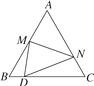
    查看答案和解析>>

    科目：初中数学 来源： 题型：

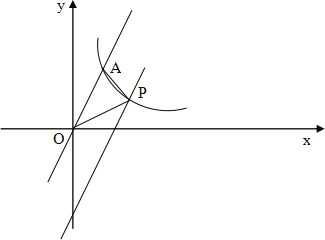
    【题目】如图，在平面直角坐标系中，直线y=2x与反比例函数y=在第一象限内的图像交于点A（m，2），将直线y=2x向下平移后与反比例函数y=在第一象限内的图像交于点P，且△POA的面积为2.

    （1）求k的值；

    （2）求平移后的直线的函数解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)操作发现：

    如图①'在正方形ABCD中，过A点有直线AP，点B关于AP的对称点为E，连接DE交AP于点F,当∠BAP=20°时，则∠AFD= °；当∠BAP=α°(0<α<45°)时，则∠AFD= °；猜想线段DF, EF, AF之间的数量关系：DF-EF= AF（填系数）；

    (2)数学思考：

    如图②,若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=120°”，其他条件不变，则∠AFD= °；线段DF, EF, AF之间的数量关系是否发生改变，若发生改变，请写出数量关系并说明理由；

    (3)类比探究：

    如图③，若将“正方形ABCD中”改成“菱形ABCD中，∠BAD=α°”，其他条件不变，则∠AFD= °；请直接写出线段DF,EF,AF之间的数量关系： .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

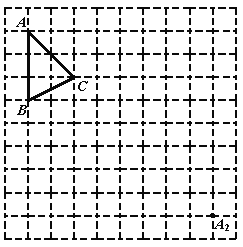
    【题目】如图，是一个由边长为1的小正方形组成的10×10的正方形网格，

    （1）在网格中画出将△ABC向右平移4个单位后的△A1B1C1；

    （2）△ABC绕点O旋转180°后，点A与点A2重合，请在网格中画出点O，并画出△ABC绕点O旋转180°后的△A2B2C2；

    （3）描述△A1B1C1与△A2B2C2的位置关系是 ．

    查看答案和解析>>

    同步练习册答案