
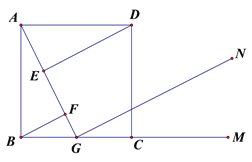
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
【答案】(1)证明见解析;
(2)作图见解析,证明见解析.
【解析】解:∵ 四边形ABCD是正方形
∴ AB=BC=CD=DA
∠DAB=∠ABC=90°
 ∴ ∠DAE+∠GAB=90°
∴ ∠DAE+∠GAB=90°
∵ DE⊥AG BF⊥AG
∴ ∠AED=∠BFA=90°
∠DAE +∠ADE=90°
∴ ∠GAB =∠ADE
在△ABF和△DAE中
∴ △ABF≌△DAE
(2)作图略
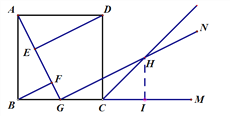 方法1:作HI⊥BM于点I
方法1:作HI⊥BM于点I
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGI=90°
∵ HI⊥BM
∴ ∠GHI+∠HGI=90°
∴ ∠AGB =∠GHI
∵ G是BC中点
∴ tan∠AGB=![]()
∴ tan∠GHI= tan∠AGB=![]()
∴ GI=2HI
∵ CH平分∠DCM
∴ ∠HCI=![]()
∴ CI=HI
∴ CI=CG=BG=HI
在△ABG和△GIH中
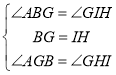
∴ △ABG≌△GIH
∴ AG=GH


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图①'在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD= °;当∠BAP=α°(0<α<45°)时,则∠AFD= °;猜想线段DF, EF, AF之间的数量关系:DF-EF= AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD= °;线段DF, EF, AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD= °;请直接写出线段DF,EF,AF之间的数量关系: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
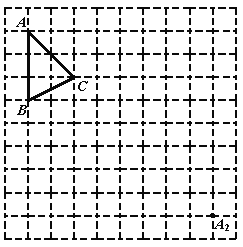
【题目】如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
(Ⅰ)如图①,若∠OCA=60°,求OD的长;
(Ⅱ)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com