
【题目】已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
(Ⅰ)如图①,若∠OCA=60°,求OD的长;
(Ⅱ)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)如图①,先由切线得∠OAB+∠BAC=90°,再利用OC⊥OB的∠BOC=90°,然后根据对顶角相等和等腰三角形的形式可求解;
(2)先判断△OEB为等腰直角三角形,得到∠OBE=∠OEB=45°,然后根据平行线的性质可得∠DAC=∠ADC,可得AC=CD=1,OC=![]() OA=
OA=![]() ,由此得解.
,由此得解.
试题解析:(1)∵AC与⊙O相切,∴∠OAC=90°.
∵∠OCA=60°,∴∠AOC=30°.∵OC⊥OB,∴∠AOB=∠AOC+∠BOC=120°.
∵OA=OB,∴∠OAB=∠OBA=30°,∴OD=AD,∠DAC=60°∴AD=CD=AC.
∵OA=1,∴OD=AC=OAtan∠AOC=![]() .
.
(2)∵OC⊥OB,∴∠OBE=∠OEB=45°.∵BE∥OA,∴∠AOC=45°,∠ABE=∠OAB,
∴OA=AC,∠OAB=∠OBA=22.5°,∴∠ADC=∠AOC+∠OAB=67.5°.
∵∠DAC=90°﹣∠OAB=67.5°=∠ADC,∴AC=CD.∵OC=![]() =
=![]() ,∴OD=OC﹣CD=
,∴OD=OC﹣CD=![]() ﹣1.
﹣1.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
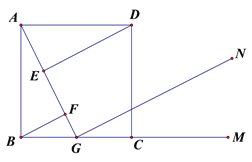
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽取了20个测量其直径,进行数据处理后,发现三组数据的平均数都是60mm,它们的方差依次为S甲2=0.612,S乙2=0.058,S丙2=0.149,根据以上提供的信息,你认为生产螺丝的质量最好的是__机床.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F. 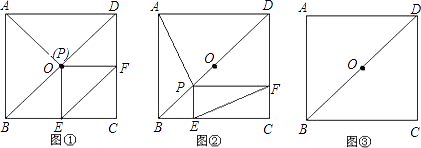
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com