
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
【答案】(1)口袋里有2个红球;
(2)列表见解析,P(一个白球一个红球)![]() .
.
【解析】(1)设红球有x个,根据任意摸出一个球,恰好摸到红球的概率等于![]() ,求出x的值即可.
,求出x的值即可.
(2)列表得出所有等可能的情况数,找出两次摸到的球中一个是红球和一个是白球的情况数,即可求出所求的概率.
解:(1)4个小球中恰好摸到红球的概率等于![]() .
.
则![]() ,解得x=2个,即口袋里有2个红球;
,解得x=2个,即口袋里有2个红球;
(2)列表如下:
红 | 红 | 白 | 白 | |
红 | ﹣﹣﹣ | (红,红) | (白,红) | (白,红) |
红 | (红,红) | ﹣﹣﹣ | (白,红) | (白,红) |
白 | (红,白) | (红,白) | ﹣﹣﹣ | (白,白) |
白 | (红,白) | (红,白) | (白,白) | ﹣﹣﹣ |
所有等可能的情况有12种,其中两次摸到的球中一个是红球和一个是白球有8种可能,则P(一个白球一个红球)![]() .
.
“点睛”此题考查的是用列表法或树状法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适用于两步完成的事件;树状法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:
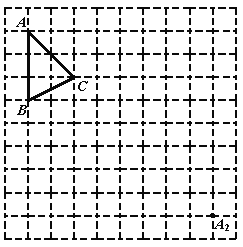
【题目】如图,是一个由边长为1的小正方形组成的10×10的正方形网格,
(1)在网格中画出将△ABC向右平移4个单位后的△A1B1C1;
(2)△ABC绕点O旋转180°后,点A与点A2重合,请在网格中画出点O,并画出△ABC绕点O旋转180°后的△A2B2C2;
(3)描述△A1B1C1与△A2B2C2的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表.某人住院治疗后得到保险公司报销金额是1100元,那么此人住院的医疗费是( )
住院医疗费(元) | 报销率(%) |
不超过500元的部分 | 0 |
超过500~1000元的部分 | 60 |
超过1000~3000元的部分 | 80 |
…… |
A.1000元
B.1250元
C.1500元
D.2000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在半径为1的⊙O上,直线AC与⊙O相切,OC⊥OB,连接AB交OC于点D.
(Ⅰ)如图①,若∠OCA=60°,求OD的长;
(Ⅱ)如图②,OC与⊙O交于点E,若BE∥OA,求OD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(101)2表示二进制数,将它转换成十进制的形式是:1×22+0×21+1×20=5,那么将二进制数(10101)2转换成十进制数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数![]() (x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
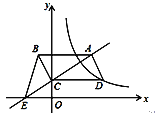
A. 2 B. ﹣2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com