
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数![]() (x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
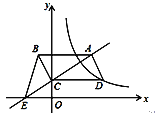
A. 2 B. ﹣2 C. 3 D. 4
【答案】D
【解析】连接ED、OD,由平行四边形的性质可得出BC=AD,AD⊥AC,根据同底等高的三角形面积相等即可得出S△BCE=S△DCE,同理得出S△OCD=S△DCE,再利用反比例函数系数K几何意义即可求出结论.
解:连接ED、OD,如图所示,
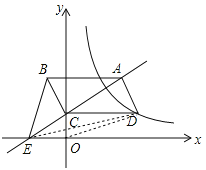
∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∵BC⊥AC,
∴AD⊥AC,
∵S△BCE和S△DCE有相同的底CE,相等的高BC=AD,
∴S△OCD=S△DCE,
∵CD平行于x轴,
∴△OCD与△ECD有相等的高,
∴S△OCD=S△DCE=S△BCE=2=![]() ,
,
∴![]() ,
,
∵反比例函数在第一象限有图象,
∴![]() ,
,
故选:D.
“点睛”本题考查了反比例函数系数K何意义、平行四边形的性质以及平行线的性质,利用同底等高的三角形面积相等找出S△OCD=S△DCE=S△BCE是解题的关键.


科目:初中数学 来源: 题型:
【题目】甲、乙、丙三台机床生产直径为60mm的螺丝,为了检验产品质量,从三台机床生产的螺丝中各抽取了20个测量其直径,进行数据处理后,发现三组数据的平均数都是60mm,它们的方差依次为S甲2=0.612,S乙2=0.058,S丙2=0.149,根据以上提供的信息,你认为生产螺丝的质量最好的是__机床.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个球,分别是红球和白球,这些球除颜色外都相同,将球搅匀,先从中任意摸出一个球,恰好摸到红球的概率为![]() .
.
(1)求口袋中有几个红球?
(2)先从中任意摸出一个球,从余下的球中再摸出一个球,请用列表法或树状图法求两次摸到的球中一个是红球和一个是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
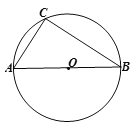
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中,是真命题的是( )
A. 相等的角是对顶角
B. 两条直线被第三条直线所截,同位角相等
C. 如果一个角的两边分别平行于另一个角的两边,那么这两个角相等
D. 在同一平面内,垂直于同一条直线的两条直线互相平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com