
 如图,△ABC和△DEF都是等边三角形,点D、E、F分别在边AB、BC、AC上,BH⊥DE于H,交AC于G,求证:AG+CF=2BD.
如图,△ABC和△DEF都是等边三角形,点D、E、F分别在边AB、BC、AC上,BH⊥DE于H,交AC于G,求证:AG+CF=2BD. 分析 如图,在CA上取一点K,使得CE=CK,连接EK,DK,BK交DE于I,连接FI.首先证明四边形DBEK是平行四边形,推出DI=IE,BI=IK,推出FI∥BG,推出FG=FK,
推出AF-AG=FC-KC,即BD-AG=CF-BD,由此即可证明.
解答 证明:如图,在CA上取一点K,使得CE=CK,连接EK,DK,BK交DE于I,连接FI.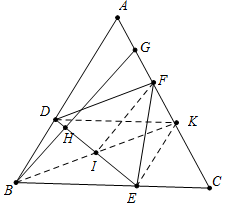
∵△ABC,△DEF都是等边三角形,
∴AB=BC=AC,DE=DF=EF,∠A=∠B=∠C=60°,∠DEF=∠DFE=∠EDF=60°,
∴∠BDE+∠BED=120°,∠BED+∠FEC=120°,
∴∠BDE=∠FEC,
在△BDE和△CEF中,
$\left\{\begin{array}{l}{∠DBE=∠C}\\{∠BDE=∠FEC}\\{DE=EF}\end{array}\right.$,
∴△BDE≌△CEF,
∴BD=CE,同理可证AF=EC,
∵CE=CK,∠C=60°,
∴△EKC是等边三角形,
∴∠KEC=∠ABC=60°,EC=EK=BD,
∴BD∥EK,BD=EK,
∴四边形DBEK是平行四边形,
∴DI=IE,BI=IK,
∵FD=FE,
∴FI⊥DE,
∵BG⊥DE,
∴FI∥BG,∵BI=IK,
∴FG=FK,
∴AF-AG=FC-KC=FC-AF,
∴BD-AG=FC-BD,
∴AG+CF=2BD.
点评 本题考查等边三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质、平行线等分线段定理等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,题目比较难,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
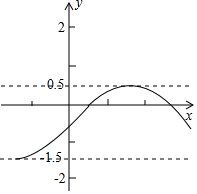 对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$.
对于某一函数,给出如下定义:若存在实数M>0,对于一函数任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的确界值.例如如图所示的函数是有界函数,其确界值是1.5.问:将函数y=-x2(-m≤x≤1,m≥o)的图象向上平移m个单位,得到的函数的确界值是t,当m在什么范围时,满足$\frac{3}{4}≤t≤1$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com