
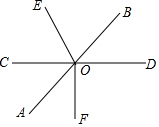
 如图,直线AB,CD相交于点O,OE平分∠BOC,OF平分∠COD,若OB将∠DOE分成2:3两部分,求∠AOF的度数.
如图,直线AB,CD相交于点O,OE平分∠BOC,OF平分∠COD,若OB将∠DOE分成2:3两部分,求∠AOF的度数. 分析 先由OE平分∠BOC,得出∠BOC=2∠BOE,再由∠DOE被一直线分成2:3两部分,结合图形可知∠DOB:∠BOE=2:3,或∠DOB:∠BOE=3:2;如果设∠BOD=2x或=3x,根据平角的定义得出∠COD=180°,列出关于x的方程,解方程求出∠DOB的度数,由对顶角相等得出∠AOC=∠BOD,然后根据OF⊥CD可知∠AOF与∠AOC互余.
解答 解:∵OE平分∠BOC,
∴∠BOC=2∠BOE,
∵∠DOE被一直线分成2:3两部分,
∴∠DOB:∠BOE=2:3或∠DOB:∠BOE=3:2;
若∠DOB:∠BOE=2:3,设∠BOD=2x,则∠BOE=3x,∠BOC=6x,
∵∠COD=180°,
∴2x+6x=180°,
∴2x=45°.
∴∠DOB=45°,
∴∠AOC=∠BOD=45°,
∵OF平分∠COD,
∴∠AOF=90°-∠AOC=45°.
若∠DOB:∠BOE=3:2,设∠BOD=3x,则∠BOE=2x,∠BOC=4x,
∵∠COD=180°,
∴3x+4x=180°,
∴x=($\frac{180}{7}$)°.
∴∠DOB=($\frac{540}{7}$)°,
∴∠AOC=∠BOD=($\frac{540}{7}$)°,
∵OF⊥CD,
∴∠AOF=90°-∠AOC=($\frac{90}{7}$)°.
点评 本题考查了垂直、角平分线、平角的定义,对顶角相等的性质,难度适中,利用数形结合及方程思想是解题的关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且DA的延长线与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且DA的延长线与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
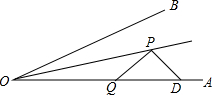 如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=3.
如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com