
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

【答案】(1)直线AD的解析式为:y=x+1;
(2)△FGH周长的最大值为![]() ;
;
(3)□APQM面积为5或10.
【解析】试题分析:(1)根据抛物线解析式求得点A、B、C点坐标,由点D,C关于抛物线的对称轴对称得点D坐标,继而利用待定系数法求解可得;
(2)设点F(x,-x2+2x+3),根据FH∥x轴及直线AD的解析式y=x+1可得点H(-x2+2x+2,-x2+2x+3),继而表示出FH的长度,根据二次函数的性质可得FH的最值情况,易得△FGH为等腰直角三角形,从而可得其周长的最大值;
(3)设P(0,p),根据平行四边形性质及点M坐标可得Q(2,4+p),分P点在AM下方与P点在AM上方两种情况,根据重合部分的面积关系及对称性求得点P的坐标后即可得APQM面积.
试题解析:(1)令-x2+2x+3=0,
解得x1=-1,x2=3,
∴A(-1,0),C(0,3),
∵点D,C关于抛物线的对称轴对称,
∴D(2,3),
∴直线AD的解析式为:y=x+1;
(2)设点F(x,-x2+2x+3),
∵FH∥x轴,
∴H(-x2+2x+2,-x2+2x+3),
∴FH=-x2+2x+2-x=-(x-![]() )2+
)2+![]() ,
,
∴FH的最大值为![]() ,
,
由直线AD的解析式为:y=x+1可知∠DAB=45°,
∵FH∥AB,
∴∠FHG=∠DAB=45°,
∴FG=GH=![]() ×
×![]() =
=![]()
故△FGH周长的最大值为![]() ×2+
×2+![]() =
=![]() ;
;
(3)①当P点在AM下方时,如图,
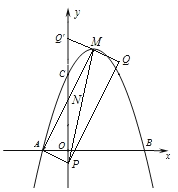
设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与□APQM重合部分的面积是□APQM面积的![]() ,
,
∴PQ′必过AM中点N(0,2),
∴可知Q′在y轴上,易知QQ′的中点T的横坐标为1,而点T必在直线AM上,
故T(1,4),从而T、M重合,
故□APQM是矩形,
易得直线AM解析式为:y=2x+2,
∴直线QQ′:y=-![]() x+
x+![]() ,
,
∴4+p=-![]() ×2+
×2+![]() ,∴p=-
,∴p=-![]() ,(注:此处也可用AM2+AP2=MP2得出p=-
,(注:此处也可用AM2+AP2=MP2得出p=-![]() ),∴PN=
),∴PN=![]() ,
,
∴S□APQM=2S△AMP=4S△ANP=4×![]() ×PN×AO=4×
×PN×AO=4×![]() ×
×![]() ×1=5;
×1=5;
②当P点在AM上方时,如图,

设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与□APQM重合部分的面积是□APQM面积的![]() ,
,
∴PQ′必过QM中点R(![]() ,4+
,4+![]() ),
),
易得直线QQ′:y=-![]() x+p+5,
x+p+5,
联立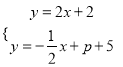 解得:x=
解得:x=![]() ,y=
,y=![]() ,
,
∴H(![]() ,
, ![]() ),
),
∵H为QQ′中点,故易得Q′(![]() ,
, ![]() ),
),
由P(0,p)、R(![]() ,4+
,4+![]() )易得直线PR解析式为:y=(
)易得直线PR解析式为:y=(![]() -
-![]() )x+p,
)x+p,
将Q′(![]() ,
, ![]() )代入到y=(
)代入到y=(![]() -
-![]() )x+p得:
)x+p得:
![]() =(
=(![]() -
-![]() )×
)×![]() +p,
+p,
整理得:p2-9p+14=0,解得p1=7,p2=2(与AM中点N重合,舍去),
∴P(0,7),∴PN=5,
∴S□APQM=2S△AMP=2×![]() ×PN×∣xM -xA∣=2×
×PN×∣xM -xA∣=2×![]() ×5×2=10.
×5×2=10.
综上所述,□APQM面积为5或10


科目:初中数学 来源: 题型:
【题目】将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图1)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图2)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件?若能,请计算出图1中的小路的宽和图2中扇形的半径;若不能符合条件,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有一个内角是锐角的三角形是锐角三角形B.钝角三角形的三个内角都是钝角
C.有一个内角是直角的三角形是直角三角形D.三条边都相等的三角形称为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
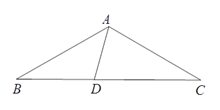
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会实践活动中,某中学对甲、乙,丙、丁四个超市三月份的苹果价格进行调查.它们的价格的平均值均为3.50元,方差分别为S甲2=0.3,S乙2=0.4,S丙2=0.1,S丁2=0.25.三月份苹果价格最稳定的超市是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,E,F分别是AB,AD的中点,DE,BF相交于点G,连接BD,CG,有下列结论:①∠BGD=120° ;②BG+DG=CG;③△BDF≌△CGB;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
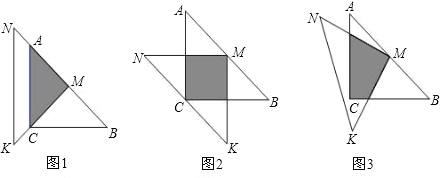
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列正确说法的个数是( )
①同位角相等;②等角的补角相等;③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是()
A.垂线段最短
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一直线的两条直线平行
D.不等式两边加同一个数,不等号的方向不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com