
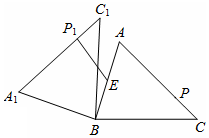
 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B旋转,得到△A1BC1.如图,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B旋转过程中,点P的对应点是点P1,线段EP1长度的取值范围为$\frac{{5\sqrt{2}}}{2}-2≤E{P_1}≤7$.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B旋转,得到△A1BC1.如图,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B旋转过程中,点P的对应点是点P1,线段EP1长度的取值范围为$\frac{{5\sqrt{2}}}{2}-2≤E{P_1}≤7$. 分析 由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值
解答 解:①如图1,过点B作BD⊥AC于点D,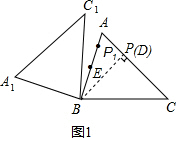
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=5×$\frac{\sqrt{2}}{2}$=$\frac{5\sqrt{2}}{2}$,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1-BE=BD-BE=$\frac{5\sqrt{2}}{2}$-2;
②如图2,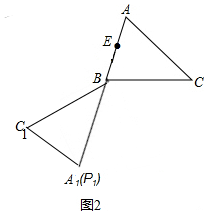
当P在AC上运动至点A,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BA1+BE=5+2=7,
综上,线段EP1长度的取值范围为$\frac{5\sqrt{2}}{2}$-2≤EP1≤7,
故答案为:$\frac{5\sqrt{2}}{2}$-2≤EP1≤7.
点评 此题考查了旋转的性质以及三角函数的应用.解题的关键是注意数形结合思想的应用,注意旋转前后的对应关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
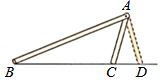 如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.
如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )
如图是一个长18cm,宽15cm的矩形图案,其中有两条宽度相等,互相垂直的彩条,彩条所占面积是图案面积的三分之一.设彩条的宽度为x cm,则下列方程正确的是( )| A. | 18x+15x-x2=$\frac{1}{3}$×15×18 | B. | (18-x)(15-x)=$\frac{1}{3}$×15×18 | ||
| C. | 18x+15x=$\frac{1}{3}$×15×18 | D. | 18x+15x+x2=$\frac{1}{3}$×15×18 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,关于线段、射线、直线的条数,说法正确的是( )
如图,关于线段、射线、直线的条数,说法正确的是( )| A. | 五条线段,三条射线 | B. | 一条射线,三条线段 | ||
| C. | 三条线段,三条射线 | D. | 三条线段,两条射线,一条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
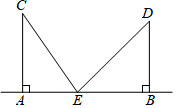 为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.
为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com