
【题目】如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.

【答案】(1)y=﹣![]() ,y=
,y=![]() x﹣2;(2)AC=CD, AC⊥CD,理由见解析;(3)45°.
x﹣2;(2)AC=CD, AC⊥CD,理由见解析;(3)45°.
【解析】分析:(1)由A点坐标可求得OA的长,再利用三角函数的定义可求得OC的长,可求得C、D点坐标,再利用待定系数法可求得直线AC的解析式;
(2)由条件可证明△OAC≌△BCD,再由角的和差可求得∠OAC+∠BCA=90°,可证得AC⊥CD;(3)连接AD,可证得四边形AEBD为平行四边形,可得出△ACD为等腰直角三角形,则可求得答案.
本题解析:
(1)∵A(5,0),∴OA=5.∵tan∠OAC=![]() ,∴
,∴![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),∴BD=OC=2,∵B(0,3),BD∥x轴,∴D(﹣2,3),
∴m=﹣2×3=﹣6,∴y=﹣![]() ,
,
设直线AC关系式为y=kx+b,∵过A(5,0),C(0,﹣2),
∴![]() ,解得
,解得 ,∴y=
,∴y=![]() x﹣2;
x﹣2;
(2)∵B(0,3),C(0,﹣2),∴BC=5=OA,
在△OAC和△BCD中
 ,∴△OAC≌△BCD(SAS),∴AC=CD,
,∴△OAC≌△BCD(SAS),∴AC=CD,
∴∠OAC=∠BCD,∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,

∵AE=OC,BD=OC,AE=BD,∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,∴∠BMC=∠DAC,
∵△OAC≌△BCD,∴AC=CD,
∵AC⊥CD,∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的“学习交通安全知识,争做文明中学生”主题活动月中,学校德工处随机选取了该校部分学生,对闯红灯情况进行了一次调查,调查结果有三种情况:A.从不闯红灯;B.偶尔闯红灯;C经常闯红灯.德工处将调查的数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,回答下列问题:
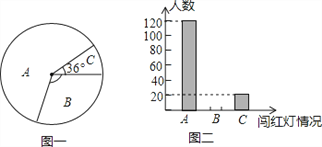
(1)本次活动共调查了_______名学生;
(2)请补全(图二),并求(图一)中 B区域的圆心角的度数_______;
(3)若该校有2400名学生,请估算该校 不严格遵守信号灯指示的有____人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1,B1,C1的坐标.
(2)以格点为三角形顶点,,在网格内画出△A2B2C2,使△ABC∽△A2B2C2 ,相似比为 ![]()
![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com