
 已知a,b,c在数轴上的位置如图所示.
已知a,b,c在数轴上的位置如图所示.分析 (1)根据数轴可以判断a、b、c的大小,从而可以解答本题;
(2)根据a、b、c的大小,可以将式子:|a+1|-|c-b|+|b-1|+|b-a|中的绝对值符号去掉,从而可以解答本题;
(3)根据a+b+c=0,且b与-1的距离和c与-1的距离相等,可以得到a的值和b+c的值,从而可以得到-a2+2b-c-(a-4c-b)的值.
解答 解:(1)由数轴可得,
c<-1<0<b<1<a,
∴a,b之间的距离为a-b,b,c之间的距离为b-c,a,c之间的距离为a-c,
故答案为:a-b,b-c,a-c;
(2)∵c<-1<0<b<1<a,
∴|a+1|-|c-b|+|b-1|+|b-a|
=a+1+c-b+1-b+a-b
=2a-3b+c+2;
(3)∵a+b+c=0,b与-1的距离和c与-1的距离相等,c<-1<0<b<1<a,
∴b-(-1)=-1-c,
∴b+1=-1-c,
∴b+c=-2,a=(-b+c)=2,
∴-a2+2b-c-(a-4c-b)
=-a2+2b-c-a+4c+b
=-a2+3b+3c-a
=-22+3(b+c)-2
=-4-6-2
=-12.
点评 本题考查整式的加减、绝对值、数轴,解题的关键是明确数轴的特点,会去绝对值符号,利用数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
| A. | 近似数2万与20 000的精确度相同 | B. | 近似数0.001精确到千分位 | ||
| C. | 0.6749精确到百分位是0.675 | D. | 近似数38与38.0的精确度相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.
如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
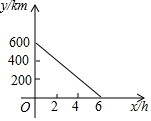 甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:
甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com