
【题目】已知直线l:y=kx(k<0),将直线y=kx沿y轴向下平移m(m>0)个单位得到直线y=kx﹣m,平移后的直线与抛物线y=ax2相交于A(x1 , y1),B(x2 , y2)两点,抛物线y=ax2经过点P(6,﹣9).
(1)求a的值;
(2)如图1,当∠AOB<90°时,求m的取值范围;
(3)如图2,将抛物线y=ax2向右平移一个单位,再向上平移n个单位(n>0).若第一象限的抛物线上存在点M,N两点,且M,N两点关于直线y=x轴对称,求n的取值范围.
【答案】
(1)
解:∵抛物线y=ax2经过点P(6,﹣9),
∴36a=﹣9,
解得a=﹣ ![]()
(2)
解:将y=kx﹣m代入y=﹣ ![]() x2,得
x2,得 ![]() x2+kx﹣m=0,
x2+kx﹣m=0,
∵y=kx﹣m与抛物线y=﹣ ![]() x2相交于A(x1,y1),B(x2,y2)两点,
x2相交于A(x1,y1),B(x2,y2)两点,
∴y1=﹣ ![]() x12,y2=﹣
x12,y2=﹣ ![]() x22,x1x2=﹣4m,
x22,x1x2=﹣4m,
∴y1y2=(﹣ ![]() x12)(﹣
x12)(﹣ ![]() x22)=
x22)= ![]() (﹣4m)2=m2.
(﹣4m)2=m2.
当∠AOB=90°时,如图1,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.
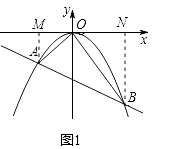
在△AOM与△OBN中,
![]() ,
,
∴△AOM∽△OBN,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y1y2=﹣x1x2,
∴m2=4m,
∵m>0,
∴m=4,
∴当∠AOB<90°时,m>4
(3)
解:∵M,N两点关于直线y=x轴对称,
∴直线y=x是线段MN的垂直平分线,
∴直线MN的斜率为﹣1,OM=ON,
∴∠MOP=∠NOP,
∵∠GOP=∠HOP=45°,
∴∠GOM=∠HON.
如图2,设直线MN的解析式为y=﹣x+b,与平移后的抛物线y=﹣ ![]() (x﹣1)2+n交于M、N两点,交x轴于E点.分别过M,N作y轴、x轴垂线,垂足分别为G、H,
(x﹣1)2+n交于M、N两点,交x轴于E点.分别过M,N作y轴、x轴垂线,垂足分别为G、H,
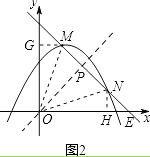
设M(m1,n1),N(m2,n2),直线MN与直线y=x交于点P.
在△OMG与△ONH中,
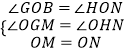 ,
,
∴△OMG≌△ONH,
∴MG=HN,即MG=HE.
将y=﹣ ![]() (x﹣1)2+n代入y=﹣x+b得:
(x﹣1)2+n代入y=﹣x+b得: ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() +b﹣n=0,
+b﹣n=0,
由根与系数的关系得m1+m2=6,
∵OE=HE+OH=MG+OH=m1+m2=6,
∴b=6.
即 ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ﹣n=0,
﹣n=0,
∵△>0,
∴(﹣ ![]() )2﹣4×
)2﹣4× ![]() ×(
×( ![]() ﹣n)>0,
﹣n)>0,
解得n>4.
又M,N在第一象限,
∴m1m2=4( ![]() ﹣n)>0,
﹣n)>0,
解得n< ![]() ,
,
∴n的取值范围是4<n< ![]()
【解析】(1)将点P(6,﹣9)的坐标代入y=ax2 , 即可求出a的值;(2)将y=kx﹣m代入y=﹣ ![]() x2 , 得
x2 , 得 ![]() x2+kx﹣m=0,根据二次函数图象上点的坐标特征以及根与系数的关系得出y1=﹣
x2+kx﹣m=0,根据二次函数图象上点的坐标特征以及根与系数的关系得出y1=﹣ ![]() x12 , y2=﹣
x12 , y2=﹣ ![]() x22 , x1x2=﹣4m,那么y1y2=m2 . 当∠AOB=90°时,如图1,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.证明△AOM∽△OBN,根据相似三角形对应边成比例得出y1y2=﹣x1x2 , 依此列出关于m的方程,求出m的值,进而得出当∠AOB<90°时,m的取值范围;(3)根据轴对称的性质得出直线y=x是线段MN的垂直平分线,如图2,设直线MN的解析式为y=﹣x+b,与平移后的抛物线y=﹣
x22 , x1x2=﹣4m,那么y1y2=m2 . 当∠AOB=90°时,如图1,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N.证明△AOM∽△OBN,根据相似三角形对应边成比例得出y1y2=﹣x1x2 , 依此列出关于m的方程,求出m的值,进而得出当∠AOB<90°时,m的取值范围;(3)根据轴对称的性质得出直线y=x是线段MN的垂直平分线,如图2,设直线MN的解析式为y=﹣x+b,与平移后的抛物线y=﹣ ![]() (x﹣1)2+n交于M、N两点,交x轴于E点,分别过M,N作y轴、x轴垂线,垂足分别为G、H,设M(m1 , n1),N(m2 , n2).利用AAS证明△OMG≌△ONH,得出MG=HN,即MG=HE.将y=﹣
(x﹣1)2+n交于M、N两点,交x轴于E点,分别过M,N作y轴、x轴垂线,垂足分别为G、H,设M(m1 , n1),N(m2 , n2).利用AAS证明△OMG≌△ONH,得出MG=HN,即MG=HE.将y=﹣ ![]() (x﹣1)2+n代入y=﹣x+b得:
(x﹣1)2+n代入y=﹣x+b得: ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() +b﹣n=0,由根与系数的关系得m1+m2=6,则b=6,那么
+b﹣n=0,由根与系数的关系得m1+m2=6,则b=6,那么 ![]() x2﹣
x2﹣ ![]() x+
x+
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知圆:(x+cosθ)2+(y﹣sinθ)2=1,直线l:y=kx.给出下面四个命题: ①对任意实数k和θ,直线l和圆M有公共点;
②对任意实数k,必存在实数θ,使得直线l和圆M相切;
③对任意实数θ,必存在实数k,使得直线l和圆M相切;
④存在实数k和θ,使得圆M上有一点到直线l的距离为3.
其中正确的命题是(写出所以正确命题的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(1)若直线l与曲线C没有公共点,求m的取值范围;
(2)若m=0,求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD= ![]() .
. 
(1)求旗杆EF的高;
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. 
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N= . 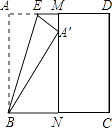
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:
(1)从中任取一球,小球上的数字为偶数
(2)从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数y=![]() 的图象上.
的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的课外阅读情况,随机抽查了10学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这10名学生周阅读所用时间,下列说法正确的是( )
A.中位数是6.5
B.众数是12
C.平均数是3.9
D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=6,点E在边CD上,DE= ![]() DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 .
DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com