
【题目】如图,抛物线顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,-3),在抛物线的对称轴上是否存在一点P,使得EP+FP最小,如果存在,求出点P的坐标;如果不存在,请说明理由.

【答案】(1)y=x2+2x+3;(2)存在,P(1,0),理由见解析;
【解析】
(1)根据顶点式可求得抛物线的表达式;
(2)根据轴对称的最短路径问题,作E关于对称轴的对称点E',连接E'F交对称轴于P,此时EP+FP的值最小,先求E'F的解析式,它与对称轴的交点就是所求的点P;
(1)设抛物线的表达式为:y=a(x1)2+4,
把(0,3)代入得:3=a(01)2+4,
解得:a=1,
∴抛物线的表达式为:y=(x1)2+4=x2+2x+3;
(2)存在,
作E关于对称轴的对称点E′,连接E′F交对称轴于P,此时EP+FP的值最小,
∵E(0,3),
∴E′(2,3),
易得E′F的解析式为:y=3x3,
当x=1时,y=3×13=0,
∴P(1,0).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
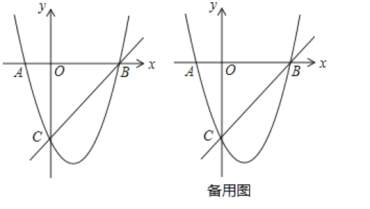
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点
下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(不要求写出自变量
之间的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() (点
(点![]() 在线段
在线段![]() 上),
上),![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
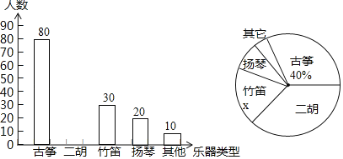
【题目】某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.
(1)这次共抽取 学生调查,扇形统计图中的x= ;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是多少度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+1与y轴交于点A,与双曲线![]() (x>0)交于点B(2,a).
(x>0)交于点B(2,a).
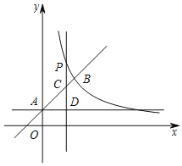
(1)求a,k的值.
(2)点P是直线l上方的双曲线上一点,过点P作平行于y轴的直线,交直线l于点C,过点A作平行于x轴的直线,交直线PC于点D,设点P的横坐标为m.
①若m=![]() ,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
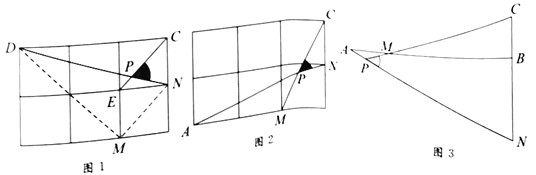
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划一次性购进甲、乙两种商品共![]() 件,甲、乙两种商品的进价和售价如下表所示:
件,甲、乙两种商品的进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 100 | 80 |
售价(元/件) | 150 | 120 |
设购进甲种商品的数量为![]() 件.
件.
(1)设进货成本为![]() 元,求
元,求![]() 与
与![]() 之间的函数解析式;若购进甲种商品的数量不少于
之间的函数解析式;若购进甲种商品的数量不少于![]() 件,则最低进货成本是多少元?
件,则最低进货成本是多少元?
(2)若除了进货成本,还要支付运费和销售员工工资共![]() 元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价
元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价![]() 元
元![]() ,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为
,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为![]() 元.
元.
①每件甲种商品的利润是 元(用含![]() 的代数式表示)
的代数式表示)
②求![]() 关于
关于![]() 的函数解析式
的函数解析式
③当![]() 时,请你根据
时,请你根据![]() 的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,![]() .
.
(1)求GC的长;
(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
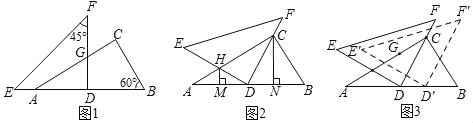
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=![]() ,则图中阴影部分面积为( )
,则图中阴影部分面积为( )
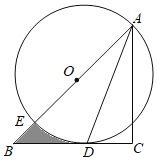
A.4﹣![]() B.2﹣
B.2﹣![]() C.2﹣πD.1﹣
C.2﹣πD.1﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,把与
中,把与![]() 轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线
轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴于点
轴于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),交
左侧),交![]() 轴于点
轴于点![]() .抛物线
.抛物线![]() 与
与![]() 是“共根抛物线”,其顶点为
是“共根抛物线”,其顶点为![]() .
.
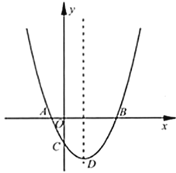
(1)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 对应的函数表达式;
对应的函数表达式;
(2)当![]() 的值最大时,求点
的值最大时,求点![]() 的坐标;
的坐标;
(3)设点![]() 是抛物线
是抛物线![]() 上的一个动点,且位于其对称轴的右侧.若
上的一个动点,且位于其对称轴的右侧.若![]() 与
与![]() 相似,求其“共根抛物线”
相似,求其“共根抛物线”![]() 的顶点
的顶点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com