
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өг![]() ОӘЧшұкФӯөгЈ¬ЕЧОпПЯ
ОӘЧшұкФӯөгЈ¬ЕЧОпПЯ![]() Ҫ»
Ҫ»![]() ЦбУЪ
ЦбУЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬Ҫ»
БҪөгЈ¬Ҫ»![]() ЦбУЪөг
ЦбУЪөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() ҫӯ№э
ҫӯ№э![]() Ј¬
Ј¬![]() БҪөгЈ®
БҪөгЈ®
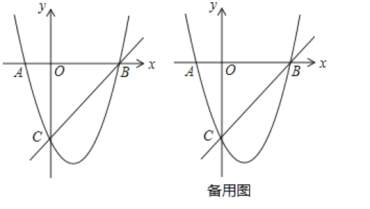
ЈЁ1Ј©ЗуЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©№эөг![]() ЧчЦұПЯ
ЧчЦұПЯ![]() ЦбҪ»ЕЧОпПЯУЪБнТ»өг
ЦбҪ»ЕЧОпПЯУЪБнТ»өг![]() Ј¬өг
Ј¬өг![]() КЗЦұПЯ
КЗЦұПЯ![]() ПВ·ҪЕЧОпПЯЙПөДТ»ёц¶ҜөгЈ¬ЗТФЪЕЧОпПЯ¶ФіЖЦбөДУТІаЈ¬№эөг
ПВ·ҪЕЧОпПЯЙПөДТ»ёц¶ҜөгЈ¬ЗТФЪЕЧОпПЯ¶ФіЖЦбөДУТІаЈ¬№эөг![]() Чч
Чч![]() ЦбУЪөг
ЦбУЪөг![]() Ј¬
Ј¬![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј¬Ҫ»
Ј¬Ҫ»![]() УЪөг
УЪөг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ј¬№эөг
Ј¬№эөг![]() Чч
Чч![]() УЪөг
УЪөг![]() Ј¬Йиөг
Ј¬Йиөг![]() өДәбЧшұкОӘ
өДәбЧшұкОӘ![]() Ј¬ПЯ¶О
Ј¬ПЯ¶О![]() өДіӨОӘ
өДіӨОӘ![]() Ј¬Зу
Ј¬Зу![]() Ул
Ул![]() Ц®јдөДәҜКэҪвОцКҪЈЁІ»ТӘЗуРҙіцЧФұдБҝ
Ц®јдөДәҜКэҪвОцКҪЈЁІ»ТӘЗуРҙіцЧФұдБҝ![]() өДИЎЦө·¶О§Ј©Ј»
өДИЎЦө·¶О§Ј©Ј»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬Б¬ҪУ![]() Ј¬№эөг
Ј¬№эөг![]() Чч
Чч![]() УЪөг
УЪөг![]() ЈЁөг
ЈЁөг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ©Ј¬
ЙПЈ©Ј¬![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ҫ»
Ҫ»![]() УЪөг
УЪөг![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬ЗуПЯ¶О
КұЈ¬ЗуПЯ¶О![]() өДіӨЈ®
өДіӨЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©
Ј»ЈЁ3Ј©![]() Ј®
Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©КЧПИЗуіцөгBЎўCөДЧшұкЈ¬И»әуАыУГҙэ¶ЁПөКэ·ЁЗуіцЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ёщҫЭSЎчABC=SЎчAMC+SЎчAMBЈ¬УЙИэҪЗРОГж»э№«КҪҝЙЗуyУлmЦ®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ3Ј©ИзНј2Ј¬УЙЕЧОпПЯ¶ФіЖРФҝЙөГDЈЁ2Ј¬-3Ј©Ј¬№эөгBЧчBKЎНCDҪ»ЦұПЯCDУЪөгKЈ¬OGЎНOSҪ»KBУЪGЈ¬ҝЙөГЛДұЯРОOCKBОӘХэ·ҪРОЈ¬№эөгOЧчOHЎНPCҪ»PCСУіӨПЯУЪөгHЈ¬ORЎНBQҪ»BQУЪөгIҪ»BKУЪөгRЈ¬ҝЙөГЛДұЯРОOHQIОӘҫШРОЈ¬ҝЙЦӨЎчOBGЎХЎчOCSЈ¬ЎчOSRЎХЎчOGRЈ¬өГөҪtanЎПQCT=tanЎПTBKЈ¬ЙиST=TD=mЈ¬ҝЙөГSK=2m+1Ј¬CS=2-2mЈ¬TK=m+1=BRЈ¬SR=3-mЈ¬RK=2-mЈ¬ФЪRtЎчSKRЦРЈ¬ёщҫЭ№ҙ№Й¶ЁАнЗуөГmЈ¬ҝЙөГtanЎПPCD=![]() Ј¬№эөгPЧчPEЎдЎНxЦбУЪEЎдҪ»CDУЪөгFЎдЈ¬өГөҪPЈЁtЈ¬-
Ј¬№эөгPЧчPEЎдЎНxЦбУЪEЎдҪ»CDУЪөгFЎдЈ¬өГөҪPЈЁtЈ¬-![]() t-3Ј©Ј¬ҝЙөГ-
t-3Ј©Ј¬ҝЙөГ-![]() t-3=t2-2t-3Ј¬ЗуөГtЈ¬ФЩёщҫЭMN=dЗуҪвјҙҝЙЈ®
t-3=t2-2t-3Ј¬ЗуөГtЈ¬ФЩёщҫЭMN=dЗуҪвјҙҝЙЈ®
ҪвЈәЈЁ1Ј©ЎЯЦұПЯy=x-3ҫӯ№эBЎўCБҪөгЈ¬
ЎаBЈЁ3Ј¬0Ј©Ј¬CЈЁ0Ј¬-3Ј©Ј¬
ЎЯy=x2+bx+cҫӯ№эBЎўCБҪөгЈ¬
Ўа![]() Ј¬
Ј¬
ҪвөГ![]() Ј¬
Ј¬
№КЕЧОпПЯөДҪвОцКҪОӘy=x2-2x-3Ј»
ЈЁ2Ј©ИзНј1Ј¬y=x2-2x-3Ј¬
y=0КұЈ¬x2-2x-3=0Ј¬
ҪвөГx1=-1Ј¬x2=3Ј¬
ЎаAЈЁ-1Ј¬0Ј©Ј¬
ЎаOA=1Ј¬OB=OC=3Ј¬
ЎаЎПABC=45ЎгЈ¬AC=![]() Ј¬AB=4Ј¬
Ј¬AB=4Ј¬
ЎЯPEЎНxЦбЈ¬
ЎаЎПEMB=ЎПEBM=45ЎгЈ¬
ЎЯөгPөДәбЧшұкОӘtЈ¬
ЎаEM=EB=3-tЈ¬
Б¬ҪУAMЈ¬
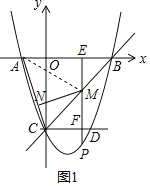
ЎЯSЎчABC=SЎчAMC+SЎчAMB
![]()
![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
ЈЁ3Ј©ИзНј2Ј¬
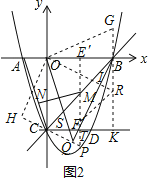
ЎЯy=x2-2x-3=ЈЁx-1Ј©2-4Ј¬
Ўа¶ФіЖЦбОӘx=1Ј¬
ЎаУЙЕЧОпПЯ¶ФіЖРФҝЙөГDЈЁ2Ј¬-3Ј©Ј¬
ЎаCD=2Ј¬
№эөгBЧчBKЎНCDҪ»ЦұПЯCDУЪөгKЈ¬
ЎаЛДұЯРОOCKBОӘХэ·ҪРОЈ¬
ЎаЎПOBK=90ЎгЈ¬CK=OB=BK=3Ј¬
ЎаDK=1Ј¬
ЎЯBQЎНCPЈ¬
ЎаЎПCQB=90ЎгЈ¬
ЎЯЎПCQB+ЎПCOB=180ЎгЈ¬
ЎаOЎўCЎўQЎўBЛДөг№ІФІЈ¬
ЎаЎПOQB=ЎПOCB=45Ўг
№эөгOЧчOHЎНPCҪ»PCСУіӨПЯУЪөгHЈ¬ORЎНBQҪ»BQУЪөгIҪ»BKУЪөгRЈ¬OGЎНOSҪ»KBУЪGЈ¬
ЎаЎПOHC=ЎПOIQ=ЎПOIB=90ЎгЈ¬
ЎаЛДұЯРОOHQIОӘҫШРОЈ¬
ЎЯЎПOQI=45ЎгЈ¬
ЎаЎПOQI=ЎПIOQ=45ЎгЈ¬
ЎЯЎПOCQ+ЎПOBQ=180ЎгЈ¬
ЎаЎПOBG=ЎПOCSЈ¬
ЎЯOB=OCЈ¬ЎПBOG=ЎПCOSЈ¬
ЎаЎчOBGЎХЎчOCSЈ¬
ЎаQG=OSЈ¬ЎПGOB=ЎПSOCЈ¬
ЎаЎПSOG=90ЎгЈ¬
ЎаЎПROG=ЎПQOI=45ЎгЈ¬
ЎЯOR=ORЈ¬
ЎаЎчOSRЎХЎчOGRЈ¬
ЎаSR=GRЈ¬
ЎаSR=CS+BRЈ¬
ЎЯЎПBOR+ЎПOBI=90ЎгЈ¬ЎПIBO+ЎПTBK=90ЎгЈ¬
ЎаЎПBOR=ЎПTBKЈ¬
ЎаtanЎПBOR=tanЎПTBKЈ¬
Ўа![]() Ј¬
Ј¬
ЎаBR=TKЈ¬
ЎЯЎПCTQ=ЎПBTKЈ¬
ЎаЎПQCT=ЎПTBKЈ¬
ЎаtanЎПQCT=tanЎПTBKЈ¬
ЙиST=TD=mЈ¬
ЎаSK=2m+1Ј¬CS=2-2mЈ¬TK=m+1=BRЈ¬SR=3-mЈ¬RK=2-mЈ¬
ФЪRtЎчSKRЦРЈ¬
ЎЯSK2+RK2=SR2Ј¬
ЎаЈЁ2m+1Ј©2+ЈЁ2-mЈ©2=ЈЁ3-mЈ©2Ј¬
ҪвөГm1=-2ЈЁЙбИҘЈ©Ј¬m2=![]() Ј»
Ј»
ЎаST=TD=![]() Ј¬TK=
Ј¬TK=![]() Ј¬
Ј¬
ЎаtanЎПTBK=![]() Ј¬
Ј¬
ЎаtanЎПPCD=![]() Ј¬
Ј¬
№эөгPЧчPEЎдЎНxЦбУЪEЎдҪ»CDУЪөгFЎдЈ¬
ЎЯCFЎд=OEЎд=tЈ¬
ЎаPFЎд=![]() tЈ¬
tЈ¬
ЎаPEЎд=![]() t+3Ј¬
t+3Ј¬
ЎаPЈЁtЈ¬-![]() t-3Ј©Ј¬
t-3Ј©Ј¬
Ўа-![]() t-3=t2-2t-3Ј¬
t-3=t2-2t-3Ј¬
ҪвөГt1=0ЈЁЙбИҘЈ©Ј¬t2=![]() Ј®
Ј®
ЎаMN=d=![]() Ј®
Ј®


 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ЁТеЈәИз№ыҪ«ЎчABCУлЎчDEFёч·ЦёоіЙБҪёцИэҪЗРОЈ¬ЗТЎчABCЛщ·ЦөДБҪёцИэҪЗРОУлЎчDEFЛщ·ЦөДБҪёцИэҪЗРО·Цұр¶ФУҰПаЛЖЈ¬ДЗГҙіЖЎчABCУлЎчDEF»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЈ¬Ҫ«ГҝМх·ЦёоПЯіЖОӘЎ°ҪьЛЖ·ЦёоПЯЎұЈ®
ЈЁ1Ј©ИзНј1Ј¬ФЪRtЎчABCәНRtЎчDEFЦРЈ¬ЎПCЈҪЎПFЈҪ90ЎгЈ¬ЎПAЈҪ30ЎгЈ¬ЎПDЈҪ40ЎгЈ¬ЗлЕР¶ПХвБҪёцИэҪЗРОКЗ·с»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЈҝИз№ыКЗЈ¬ЗлЦұҪУФЪНј1ЦР»ӯіцТ»Чй·ЦёоПЯЈ¬ІўЧўГч·ЦёоәуЛщөГБҪёцРЎИэҪЗРОИсҪЗөД¶ИКэЈ»ИфІ»КЗЈ¬ЗлЛөГчАнУЙЈ®
ЈЁ2Ј©ЕР¶ППВБРГьМвКЗХжГьМв»№КЗјЩГьМвЈ¬ИфКЗХжГьМвЈ¬ЗлФЪАЁәЕДЪҙтЎ°ЎМЎұЈ»ИфКЗјЩГьМвЈ¬ЗлФЪАЁәЕДЪҙтЎ°ЎБЎұЈ®
ўЩИОТвБҪёцЦұҪЗИэҪЗРО¶јКЗ»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЎЎ ЎЎЈ»
ўЪБҪёцЎ°ҪьЛЖИэҪЗРОЎұЦ»УРОЁТ»өДЎ°ҪьЛЖ·ЦёоПЯЎұЎЎ ЎЎЈ»
ўЫИз№ыБҪёцИэҪЗРОЦРУРТ»ёцҪЗПаөИЈ¬ДЗГҙХвБҪёцИэҪЗРОТ»¶ЁКЗ»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЎЎ ЎЎЈ®
ЈЁ3Ј©ИзНј2Ј¬ТСЦӘЎчABCУлЎчDEFЦРЈ¬ЎПAЈҪЎПDЈҪ15ЎгЈ¬ЎПBЈҪ45ЎгЈ¬ЎПEЈҪ60ЎгЈ¬ЗТBCЈҪEFЈҪ![]()
![]() Ј¬ЕР¶ПХвБҪёцИэҪЗРОКЗ·с»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЈҝИз№ыКЗЈ¬ЗлФЪНј2ЦР»ӯіцІ»Н¬О»ЦГөДЎ°ҪьЛЖ·ЦёоПЯЎұЈ¬ІўЦұҪУ·ЦұрРҙіцЎ°ҪьЛЖ·ЦёоПЯЎұөДәНЈ»Из№ыІ»КЗЈ¬ЗлЛөГчАнУЙЈ®
Ј¬ЕР¶ПХвБҪёцИэҪЗРОКЗ·с»ҘОӘЎ°ҪьЛЖИэҪЗРОЎұЈҝИз№ыКЗЈ¬ЗлФЪНј2ЦР»ӯіцІ»Н¬О»ЦГөДЎ°ҪьЛЖ·ЦёоПЯЎұЈ¬ІўЦұҪУ·ЦұрРҙіцЎ°ҪьЛЖ·ЦёоПЯЎұөДәНЈ»Из№ыІ»КЗЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ҫШРОEFGHөД¶ҘөгEЈ¬G·ЦұрФЪБвРОABCDөДұЯADЈ¬BCЙПЈ¬¶ҘөгFЈ¬HФЪБвРОABCDөД¶ФҪЗПЯBDЙПЈ®

ЈЁ1Ј©ЗуЦӨЈәBG=DEЈ»
ЈЁ2Ј©ИфEОӘADЦРөгЈ¬FH=2Ј¬ЗуБвРОABCDөДЦЬіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЦйәЈКРУРAЈ¬BЈ¬CЈ¬DЈ¬EОеёцҫ°ЗшәЬКЬУОҝНПІ°®Ј®¶ФДіРЎЗшҫУГсФЪКојЩЖЪјдИҘТФЙПОеёцҫ°ЗшВГУОЈЁЦ»СЎТ»ёцҫ°ЗшЈ©өДТвПтЧцБЛТ»ҙОЛж»ъөчІйНіјЖЈ¬ІўёщҫЭХвёцНіјЖҪб№ыЦЖЧчБЛИзПВБҪ·щІ»НкХыөДНіјЖНјЈ®
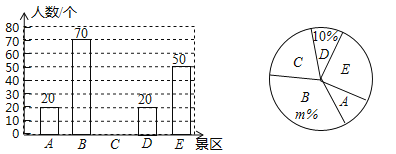
ЈЁ1Ј©ёГРЎЗшҫУГсФЪХвҙОЛж»ъөчІйЦРұ»өчІйөҪөДИЛКэКЗЎЎЎЎ ИЛЈ¬mЈҪЎЎ ЎЎЈ»
ЈЁ2Ј©ИфёГРЎЗшУРҫУГс1500ИЛЈ¬КФ№АјЖИҘCҫ°ЗшВГУОөДҫУГсФјУР¶аЙЩИЛЈҝ
ЈЁ3Ј©јЧЎўТТБҪИЛКојЩҙтЛгУОНжЈ¬јЧҙУBЎўCБҪёцҫ°өгЦРИОТвСЎФсТ»ёцУОНжЈ¬ТТҙУBЎўC ЎўEИэёцҫ°өгЦРИОТвСЎФсТ»ёцУОНжЈ®ЗујЧЎўТТЗЎәГУОНжН¬Т»ҫ°өгөДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯyЈҪk1x(xЎЭ0)УлЛ«ЗъПЯyЈҪ![]() (xЈҫ0)ПаҪ»УЪөгP(2Ј¬4)Ј®ТСЦӘөгA(4Ј¬0)Ј¬B(0Ј¬3)Ј¬Б¬ҪУABЈ¬Ҫ«RtЎчAOBСШOP·ҪПтЖҪТЖЈ¬К№өгOТЖ¶ҜөҪөгPЈ¬өГөҪЎчAЎдPBЎд.№эөгAЎдЧчAЎдCЎОyЦбҪ»Л«ЗъПЯУЪөгCЈ¬Б¬ҪУCP.
(xЈҫ0)ПаҪ»УЪөгP(2Ј¬4)Ј®ТСЦӘөгA(4Ј¬0)Ј¬B(0Ј¬3)Ј¬Б¬ҪУABЈ¬Ҫ«RtЎчAOBСШOP·ҪПтЖҪТЖЈ¬К№өгOТЖ¶ҜөҪөгPЈ¬өГөҪЎчAЎдPBЎд.№эөгAЎдЧчAЎдCЎОyЦбҪ»Л«ЗъПЯУЪөгCЈ¬Б¬ҪУCP.
(1)Зуk1Улk2өДЦөЈ»
(2)ЗуЦұПЯPCөДҪвОцКҪЈ»
(3)ЦұҪУРҙіцПЯ¶ОABЙЁ№эөДГж»эЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬¶Ҝөг
Ј¬¶Ҝөг![]() ҙУөг
ҙУөг![]() Н¬Кұіц·ўЈ¬өг
Н¬Кұіц·ўЈ¬өг![]() ТФГҝГл
ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИСШұЯ
ёцөҘО»іӨ¶ИөДЛЩ¶ИСШұЯ![]() ПтЦХөгФИЛЩФЛ¶ҜЈ¬өг
ПтЦХөгФИЛЩФЛ¶ҜЈ¬өг![]() ТФГҝГл
ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИСШұЯ
ёцөҘО»іӨ¶ИөДЛЩ¶ИСШұЯ![]() ПтЦХөгФИЛЩФЛ¶ҜЈ¬ТФ
ПтЦХөгФИЛЩФЛ¶ҜЈ¬ТФ![]() ОӘұЯФЪұЯ
ОӘұЯФЪұЯ![]() ЙП·ҪЧчХэ·ҪРО
ЙП·ҪЧчХэ·ҪРО![]() Йиөг
Йиөг![]() ФЛ¶ҜКұјдОӘ
ФЛ¶ҜКұјдОӘ![]() Ј®
Ј®
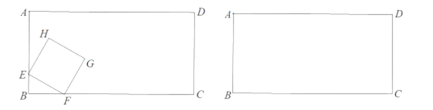
ЈЁ1Ј©УГә¬![]() өДҙъКэКҪұнКҫ
өДҙъКэКҪұнКҫ![]() Ј»
Ј»
ЈЁ2Ј©өұөг![]() ВдФЪұЯ
ВдФЪұЯ![]() ЙПКұЈ¬ЗуҙЛКұ
ЙПКұЈ¬ЗуҙЛКұ![]() өДЦөЈ»
өДЦөЈ»
ЈЁ3Ј©ЙиХэ·ҪРО![]() УлҫШРО
УлҫШРО![]() ЦШөюНјРОөДГж»эОӘ
ЦШөюНјРОөДГж»эОӘ![]() ЗлЦұҪУРҙіц
ЗлЦұҪУРҙіц![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪЈ¬ІўРҙіц
Ц®јдөДәҜКэ№ШПөКҪЈ¬ІўРҙіц![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯy1ЈҪx©Ғ5УлЛ«ЗъПЯy2ЈҪ©Ғ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦӨЈәОЮВЫpИЎәОЦөКұЈ¬БҪёцәҜКэөДНјПуәгУРБҪёцҪ»өгЈ»
ЈЁ2Ј©ЙиБҪёцҪ»өг·ЦұрОӘAЈЁx1Ј¬y1Ј©ЎўBЈЁx2Ј¬y2Ј©Ј¬ЗТВъЧгx12+x22ЈҪ3x1x2Ј¬ЗуКөКэpөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘЧи¶ПРВ№ЪТЯЗйПтРЈФ°ВыСУЈ¬И·ұЈКҰЙъЙъГь°ІИ«әНЙнМеҪЎҝөЈ¬ҪМУэІҝНЁЦӘЈ¬2020ДкҙәјҫС§ЖЪСУЖЪҝӘС§Ј¬АыУГНшЙПЖҪМЁЈ¬НЈҝОІ»НЈС§ЎұЈ¬ДіРЈ¶ФіхИэИ«МеС§ЙъКэС§ПЯЙПС§П°ЗйҝцҪшРРөчІйЈ¬Лж»ъійИЎІҝ·ЦС§ЙъөД4ФВФВХп¶ПРФІвКФіЙјЁЈ¬°ҙУЙёЯөҪөН·ЦОӘAЈ¬BЈ¬CЈ¬DЛДёцөИј¶Ј¬ёщҫЭөчІйөДКэҫЭ»жЦЖіЙИзПВөДМхРОНіјЖНјәНЙИРОНіјЖНјЈ¬ЗлёщҫЭНјЦРөДРЕПўЈ¬ҪвҙрПВБРОКМвЈә
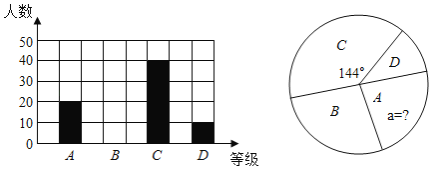
(1)ёГРЈ№ІійІйБЛЎЎ ЎЎГыН¬С§өДКэС§ІвКФіЙјЁЈ¬ЙИРОНіјЖНјЦРAөИј¶ЛщХјөД°Щ·ЦұИaЈҪЎЎ ЎЎЈ»
(2)І№И«МхРОНіјЖНјЈ»
(3)ИфёГРЈіхИэ№ІУР1180ГыН¬С§Ј¬Зл№АјЖёГРЈіхИэС§ЙъКэС§ІвКФіЙјЁУЕРгЈЁІвКФіЙјЁBј¶ТФЙПОӘУЕРгЈ¬ә¬Bј¶Ј©ФјУРЎЎ ЎЎГыЈ»
(4)ёГРЈАПКҰПлҙУБҪДРЎўБҪЕ®ЛДО»С§ЙъЦРЛж»ъСЎФсБҪО»БЛҪвЖҪКұПЯЙПС§П°ЗйҝцЈ¬ЗлУГБРұн»т»ӯКчРОНјөД·Ҫ·ЁЗуіцЗЎәГСЎЦРТ»ДРТ»Е®өДёЕВКЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯ¶ҘөгAөДЧшұкОӘЈЁ1,4Ј©Ј¬ЕЧОпПЯУлxЦбПаҪ»УЪBЎўCБҪөгЈ¬УлyЦбҪ»УЪөгEЈЁ0,3Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯөДұнҙпКҪЈ»
ЈЁ2Ј©ТСЦӘөгFЈЁ0Ј¬-3Ј©Ј¬ФЪЕЧОпПЯөД¶ФіЖЦбЙПКЗ·сҙжФЪТ»өгPЈ¬К№өГEP+FPЧоРЎЈ¬Из№ыҙжФЪЈ¬ЗуіцөгPөДЧшұкЈ»Из№ыІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com