
【题目】定义:如果将△ABC与△DEF各分割成两个三角形,且△ABC所分的两个三角形与△DEF所分的两个三角形分别对应相似,那么称△ABC与△DEF互为“近似三角形”,将每条分割线称为“近似分割线”.
(1)如图1,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,∠A=30°,∠D=40°,请判断这两个三角形是否互为“近似三角形”?如果是,请直接在图1中画出一组分割线,并注明分割后所得两个小三角形锐角的度数;若不是,请说明理由.
(2)判断下列命题是真命题还是假命题,若是真命题,请在括号内打“√”;若是假命题,请在括号内打“×”.
①任意两个直角三角形都是互为“近似三角形” ;
②两个“近似三角形”只有唯一的“近似分割线” ;
③如果两个三角形中有一个角相等,那么这两个三角形一定是互为“近似三角形” .
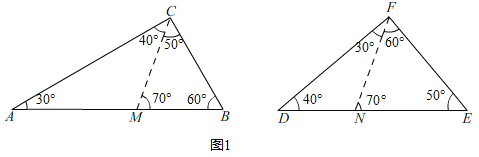
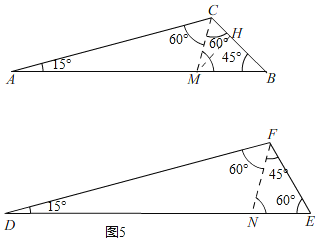
(3)如图2,已知△ABC与△DEF中,∠A=∠D=15°,∠B=45°,∠E=60°,且BC=EF=![]()
![]() ,判断这两个三角形是否互为“近似三角形”?如果是,请在图2中画出不同位置的“近似分割线”,并直接分别写出“近似分割线”的和;如果不是,请说明理由.
,判断这两个三角形是否互为“近似三角形”?如果是,请在图2中画出不同位置的“近似分割线”,并直接分别写出“近似分割线”的和;如果不是,请说明理由.
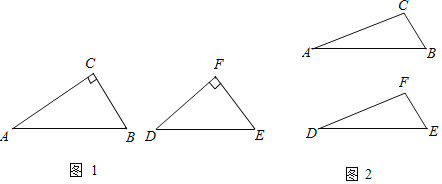
【答案】(1)这两个三角形是互为“近似三角形”,图形见解析;(2)√,×,×;(3)这两个三角形是互为“近似三角形”, “近似分割线”的和为6+4![]() 或
或![]() .
.
【解析】
(1)根据互为“近似三角形”即可得出结论;
(2)根据互为“近似三角形”的意义,判断出是假命题,画图说明即可得出结论;
(3)如图5,先判断出△BCM≌△FEN(ASA),得出CM=FN,再构造出直角三角形,即可得出结论;
②如图6,同(1)的方法即可得出结论.
解:(1)这两个三角形是互为“近似三角形”,如图1所示,
(2)①任意两个直角三角形都是互为“近似三角形”,是真命题,如图2所示,
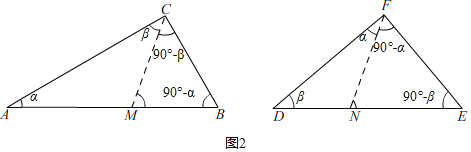
②两个“近似三角形”只有唯一的“近似分割线”,假命题,如图3所示,
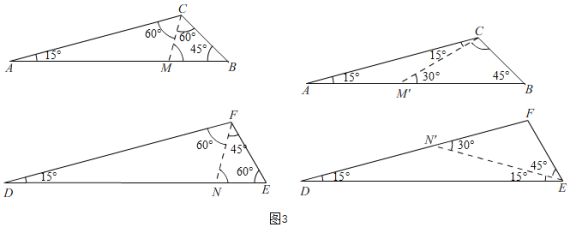
在△ABC与△DEF中,∠A=∠D=15°,∠B=45°,∠E=60°;
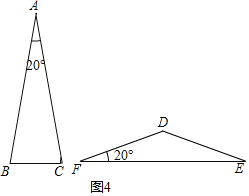
③如果两个三角形中有一个角相等,那么这两个三角形一定是互为“近似三角形”,是假命题,
如图4所示,一个顶角为20°的等腰三角形和底角为20°的等腰三角形;
 ,
,
故答案为:√,×,×;
(3)这两个三角形是互为“近似三角形”,
①如图5,
在△BCM和△FEN中,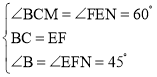 ,
,
∴△BCM≌△FEN(ASA),
∴CM=EN,FN=BM,
过点M作MH⊥BC于H,
在Rt△MHC中,设CH=x,则MH=![]() x,CM=2x,
x,CM=2x,
在Rt△BHM中,BH=MH=![]() x,
x,
∵BC=x+![]() x=
x=![]() ,
,
∴x=![]() ,
,
∴CM=2![]() ,FN=BM=
,FN=BM=![]() ,
,
∴“近似分割线”的和为CM+FN=![]() ;
;
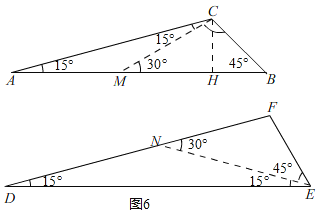
②同①的方法得,△CBM≌FEN(ASA),
∴BM=EN,
过点C作CH⊥BM于H,
在Rt△BHC中,BH=CH=![]() =1+
=1+![]() ,
,
在Rt△CHM中,CM=2CH=2+2![]() ,MH=
,MH=![]() CH=3+
CH=3+![]() ,
,
∴NE=BM=4+2![]() ,
,
∴“近似分割线”的和为CM+EN=6+4![]() ,
,
即“近似分割线”的和为6+4![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图(1)已知矩形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 点的坐标为
点的坐标为![]() ,动点
,动点![]() 以每秒2个单位长度的速度沿
以每秒2个单位长度的速度沿![]() 运动(
运动(![]() 点不与点
点不与点![]() 、点
、点![]() 重合),设运动时间为
重合),设运动时间为![]() 秒.
秒.
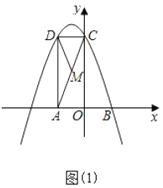
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线解析式;
三点的抛物线解析式;
(2)点![]() 在(1)中的抛物线上,当
在(1)中的抛物线上,当![]() 为
为![]() 中点时,若
中点时,若![]() ,求点
,求点![]() 的坐标;
的坐标;
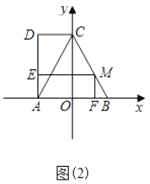
(3)当点![]() 在
在![]() 上运动时,如图(2)过点
上运动时,如图(2)过点![]() 作
作![]() ,
,![]() 轴,垂足分别为
轴,垂足分别为![]() 、
、![]() ,设矩形
,设矩形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
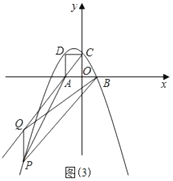
(4)如图(3)点![]() 在(1)中的抛物线上,
在(1)中的抛物线上,![]() 是
是![]() 延长线上的一点,且
延长线上的一点,且![]() 、
、![]() 两点均在第三象限内,
两点均在第三象限内,![]() 、
、![]() 是位于直线
是位于直线![]() 同侧的不同两点,若点
同侧的不同两点,若点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,
,![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
名称 | 三棱锥 | 三棱柱 | 正方体 | 正八面体 |
图形 |
|
|
|
|
顶点数V | 4 | 6 | 8 | |
棱数E | 6 | 12 | ||
面数F | 4 | 5 | 8 |
(2)分析表中的数据,你能发现V、E、F之间有什么关系吗?请写出关系式:____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年植树节期间,某景观园林公司购进一批成捆的![]() ,
,![]() 两种树苗,每捆
两种树苗,每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵,每捆
种树苗多10棵,每捆![]() 种树苗和每捆
种树苗和每捆![]() 种树苗的价格分别是630元和600元,而每棵
种树苗的价格分别是630元和600元,而每棵![]() 种树苗和每棵
种树苗和每棵![]() 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵,![]() 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进
种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进![]() 种树苗和
种树苗和![]() 种树苗各多少棵?并求出最低费用.
种树苗各多少棵?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
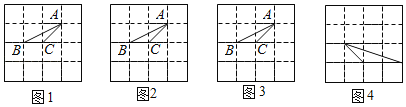
【题目】如图,为4×4的正方形网格图,△ABC的顶点都在网格格点上(每个小正方形的顶点称为格点,顶点都在格点上的三角形称为格点三角形).
(1)在图1,图2,图3中分别画一个与△ABC有一公共边且与△ABC成轴对称的三角形.
(2)在图4中画出一个满足要求的格点△DEF,要求:△DEF与△ABC相似,且相似比的值为无理数.(画出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)这次共抽取_________名学生进行统计调查,扇形统计图中,![]() 类所对应的扇形圆心角的大小为__________
类所对应的扇形圆心角的大小为__________
(2)将条形统计图补充完整
(3)该校共有1500名学生,估计该校表示“喜欢”的![]() 类的学生大约有多少人?
类的学生大约有多少人?
各类学生人数条形统计图各类学生人数扇形统计图
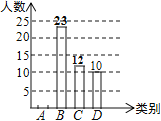
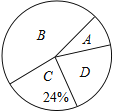
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
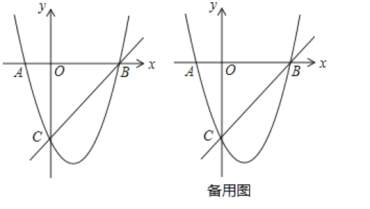
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点
下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(不要求写出自变量
之间的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() (点
(点![]() 在线段
在线段![]() 上),
上),![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com