
ЁОЬтФПЁПШчЭМЃЈ1ЃЉвбжЊОиаЮ![]() дкЦНУцжБНЧзјБъЯЕ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕуЕФзјБъЮЊ
ЕуЕФзјБъЮЊ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШби
вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШби![]() дЫЖЏЃЈ
дЫЖЏЃЈ![]() ЕуВЛгыЕу
ЕуВЛгыЕу![]() ЁЂЕу
ЁЂЕу![]() жиКЯЃЉЃЌЩшдЫЖЏЪБМфЮЊ
жиКЯЃЉЃЌЩшдЫЖЏЪБМфЮЊ![]() УыЃЎ
УыЃЎ
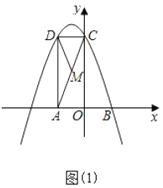
ЃЈ1ЃЉЧѓОЙ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЕФХзЮяЯпНтЮіЪНЃЛ
Ш§ЕуЕФХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() дкЃЈ1ЃЉжаЕФХзЮяЯпЩЯЃЌЕБ
дкЃЈ1ЃЉжаЕФХзЮяЯпЩЯЃЌЕБ![]() ЮЊ
ЮЊ![]() жаЕуЪБЃЌШє
жаЕуЪБЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЙ§Еу
ЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЙ§Еу![]() зї
зї![]() ЃЌ
ЃЌ![]() жсЃЌДЙзуЗжБ№ЮЊ
жсЃЌДЙзуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЩшОиаЮ
ЃЌЩшОиаЮ![]() гы
гы![]() жиЕўВПЗжУцЛ§ЮЊ
жиЕўВПЗжУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
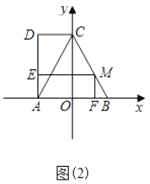
ЃЈ4ЃЉШчЭМЃЈ3ЃЉЕу![]() дкЃЈ1ЃЉжаЕФХзЮяЯпЩЯЃЌ
дкЃЈ1ЃЉжаЕФХзЮяЯпЩЯЃЌ![]() ЪЧ
ЪЧ![]() бгГЄЯпЩЯЕФвЛЕуЃЌЧв
бгГЄЯпЩЯЕФвЛЕуЃЌЧв![]() ЁЂ
ЁЂ![]() СНЕуОљдкЕкШ§ЯѓЯоФкЃЌ
СНЕуОљдкЕкШ§ЯѓЯоФкЃЌ![]() ЁЂ
ЁЂ![]() ЪЧЮЛгкжБЯп
ЪЧЮЛгкжБЯп![]() ЭЌВрЕФВЛЭЌСНЕуЃЌШєЕу
ЭЌВрЕФВЛЭЌСНЕуЃЌШєЕу![]() ЕН
ЕН![]() жсЕФОрРыЮЊ
жсЕФОрРыЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
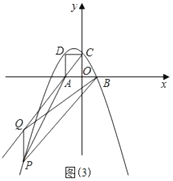
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕу
ЃЛЃЈ2ЃЉЕу![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() зюДѓ
зюДѓ![]() ЃЛЃЈ4ЃЉ
ЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжБНЧШ§НЧаЮЕФаджЪПЩЧѓЕуCЃЌЕуDзјБъЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓНтЮіЪНЃЛ
ЃЈ2ЃЉгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУDM=AMЃЌPD=APЃЌПЩЕУЕуPдкADЕФДЙжБЦНЗжЯпЩЯЃЌПЩЧѓЕуPЕФзнзјБъЃЌДњШыПЩЧѓНтЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЄЁїACBЪЧЕШБпШ§НЧаЮЃЌПЩЕУCM=2t-4ЃЌBF=![]() ЃЈ8-2tЃЉ=4-tЃЌMF=
ЃЈ8-2tЃЉ=4-tЃЌMF=![]() -
-![]() tЃЌAF=tЃЌМДПЩЧѓжиЕўВПЗжУцЛ§ЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЧѓНтЃЛ
tЃЌAF=tЃЌМДПЩЧѓжиЕўВПЗжУцЛ§ЃЌгЩЖўДЮКЏЪ§ЕФаджЪПЩЧѓНтЃЛ
ЃЈ4ЃЉЯШЧѓГіжБЯпACЃЌBPЕФНтЮіЪНЃЌМДПЩЧѓЕуPзјБъЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ
ЩшХзЮяЯпНтЮіЪНЮЊ![]() ЃЌДњ
ЃЌДњ![]() ЃЌ
ЃЌ![]()
Ёр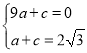 ЃЌ
ЃЌ
НтЕУЃК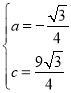 ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁп![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁїPAMЁеЁїPDMЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕу![]() дк
дк![]() ЕФДЙжБЦНЗжЯпЩЯЃЌ
ЕФДЙжБЦНЗжЯпЩЯЃЌ
ЁрЕу![]() знзјБъЮЊ
знзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕу![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁїACBЪЧЕШБпШ§НЧаЮЃЌ
гЩЬтвтПЩЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁпЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁїCMHЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() зюДѓ
зюДѓ![]() ЃЛ
ЃЛ
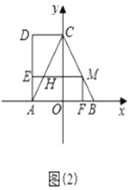
ЃЈ4ЃЉЁп![]() ЃЌгж
ЃЌгж![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЩшжБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() ЃЌАб
ЃЌАб![]() ЃЌ
ЃЌ![]() ДњШыЦфжаЃЌ
ДњШыЦфжаЃЌ
ЕУ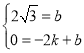 ЃЌ
ЃЌ
Ёр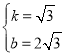 ЃЌ
ЃЌ
ЁржБЯп![]() НтЮіЪНЮЊЃК
НтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Аб![]() ДњШыЦфжаЃЌЕУ
ДњШыЦфжаЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯп![]() НтЮіЪНЮЊЃК
НтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ


 СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ
СщаЧМЦЫуаЁДяШЫЯЕСаД№АИ УЯНЈЦНДэЬтБОЯЕСаД№АИ
УЯНЈЦНДэЬтБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
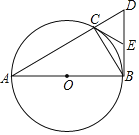
ЁОЬтФПЁПвбжЊЃКШчЭМ1ЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЌЦНаагкxжсЕФжБЯпгыИУХзЮяЯпНЛгкЕуAЃЌB(ЕуAдкЕуBзѓВр)ЃЌИљОнЖдГЦадЁїAMBКуЮЊЕШбќШ§НЧаЮЃЌЮвУЧЙцЖЈЃКЕБЁїAMBЮЊжБНЧШ§НЧаЮЪБЃЌОЭГЦЁїAMBЮЊИУХзЮяЯпЕФЁАЭъУРШ§НЧаЮЁБЃЎ
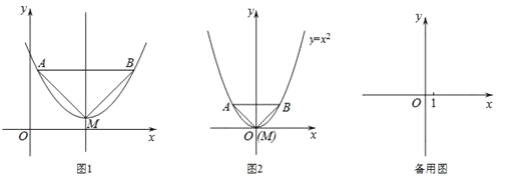
ЃЈ1ЃЉЂйШчЭМ2,ЧѓГіХзЮяЯпy=x2ЕФЁАЭъУРШ§НЧаЮЁБаББпABЕФГЄЃЛ
ЂкЧыаДГівЛИіХзЮяЯпЕФНтЮіЪНЃЌЪЙЫќЕФЭъУРШ§НЧаЮгыy=x2+1ЕФЁАЭъУРШ§НЧаЮЁБШЋЕШЃЛ
ЃЈ2ЃЉШєХзЮяЯпy=ax2+4ЕФЁАЭъУРШ§НЧаЮЁБЕФаББпГЄЮЊ4ЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉШєХзЮяЯпy=mx2+2x+n5ЕФЁАЭъУРШ§НЧаЮЁБаББпГЄЮЊn,Чвy=mx2+2x+n5ЕФзюДѓжЕЮЊ1ЃЌЧѓmЃЌnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
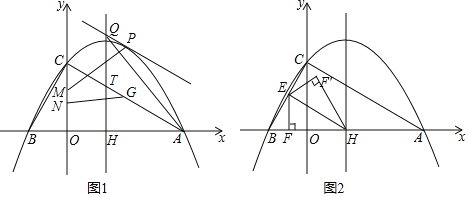
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy![]() 2
2![]() гыxжсЯрНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЌгыyжсЯрНЛгкЕуCЃЌЖдГЦжсгыxжсЯрНЛгкЕуHЃЌгыACЯрНЛгкЕуTЃЎ
гыxжсЯрНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФгвВрЃЉЃЌгыyжсЯрНЛгкЕуCЃЌЖдГЦжсгыxжсЯрНЛгкЕуHЃЌгыACЯрНЛгкЕуTЃЎ
ЃЈ1ЃЉЕуPЪЧЯпЖЮACЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуPзїPQЁЮACНЛХзЮяЯпЕФЖдГЦжсгкЕуQЃЌЕБЁїAQHУцЛ§зюДѓЪБЃЌЕуMЁЂNдкyжсЩЯЃЈЕуMдкЕуNЕФЩЯЗНЃЉЃЌMN![]() ЃЌЕуGдкжБЯпACЩЯЃЌЧѓPM+NG
ЃЌЕуGдкжБЯпACЩЯЃЌЧѓPM+NG![]() GAЕФзюаЁжЕЃЎ
GAЕФзюаЁжЕЃЎ
ЃЈ2ЃЉЕуEЮЊBCжаЕуЃЌEFЁЭxжсгкFЃЌСЌНгEHЃЌНЋЁїEFHбиEHЗелЕУЁїEF'HЃЌШчЭМЫљЪО2ЃЌдйНЋЁїEF'HбижБЯпBCЦНвЦЃЌМЧЦНвЦжаЕФЁїEF'HЮЊЁїE'FЁхH'ЃЌдкЦНвЦЙ§ГЬжаЃЌжБЯпE'H'гыxжсНЛгкЕуRЃЌдђЪЧЗёДцдкетбљЕФЕуRЃЌЪЙЕУЁїRF'H'ЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіRЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
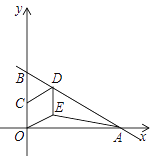
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌCЪЧOBЕФжаЕуЃЌDЪЧABЩЯвЛЕуЃЌЫФБпаЮOEDCЪЧСтаЮЃЌдђЁїOAEЕФУцЛ§ЮЊ________ЃЎ
гыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌCЪЧOBЕФжаЕуЃЌDЪЧABЩЯвЛЕуЃЌЫФБпаЮOEDCЪЧСтаЮЃЌдђЁїOAEЕФУцЛ§ЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
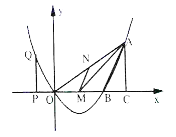
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§ЕФЭМЯѓОЙ§дЕу![]() КЭ
КЭ![]() ЃЌгы
ЃЌгы![]() жсНЛгкСэвЛЕу
жсНЛгкСэвЛЕу![]() ЃЌЧвЖдГЦжсЪЧ
ЃЌЧвЖдГЦжсЪЧ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШє![]() ЪЧ
ЪЧ![]() ЩЯЕФвЛЕуЃЌзї
ЩЯЕФвЛЕуЃЌзї![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЕФУцЛ§зюДѓЪБЃЌЧѓЕу
ЕФУцЛ§зюДѓЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉ![]() ЪЧ
ЪЧ![]() жсЩЯЕФЕуЃЌЙ§
жсЩЯЕФЕуЃЌЙ§![]() зї
зї![]() жсЃЌгыХзЮяЯпНЛгкЕу
жсЃЌгыХзЮяЯпНЛгкЕу![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() жсгк
жсгк![]() ЃЌЪЧЗёДцдкЕу
ЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙвдЕу
ЃЌЪЙвдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮгывдЕу
ЮЊЖЅЕуЕФШ§НЧаЮгывдЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЃПШєДцдкЃЌЧѓГіЕу
ЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() Фкгк
Фкгк![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЃЌНЛ
ЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФДѓаЁЃЎ
ЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
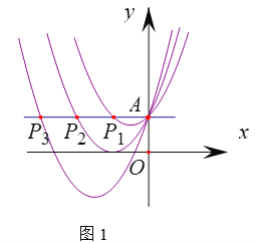
ЁОЬтФПЁПвбжЊЕуAЃЈ1ЃЌ1ЃЉдкХзЮяЯпyЃНx2+ЃЈ2m+1ЃЉxЉnЉ1ЩЯ
ЃЈ1ЃЉЧѓmЁЂnЕФЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєИУХзЮяЯпЕФЖЅЕудкxжсЩЯЃЌЧѓГіЫќЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЈnЮЊе§ећЪ§ЃЉЃЌЕуA(0ЃЌ1)ЃЎ
ЃЈnЮЊе§ећЪ§ЃЉЃЌЕуA(0ЃЌ1)ЃЎ
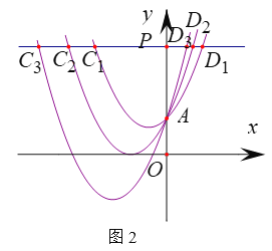
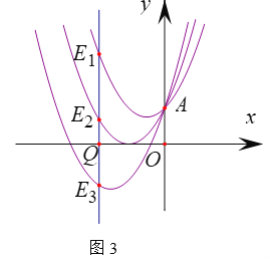
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуAзїyжсДЙЯпЃЌЗжБ№НЛХзЮяЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЈ
ЃЈ![]() КЭЕуAВЛжиКЯЃЉЃЎ
КЭЕуAВЛжиКЯЃЉЃЎ
ЂйЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЂкЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPДгЕуAГіЗЂЃЌбиyжсЯђЩЯдЫЖЏЃЌЙ§ЕуPзїyжсЕФДЙЯпЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌНЛХзЮяЯп
ЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌНЛХзЮяЯп
ЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌЁЁЃЌНЛХзЮяЯп
ЃЌЁЁЃЌНЛХзЮяЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЈ
ЃЈ![]() дкЕкЖўЯѓЯоЃЉЃЎ
дкЕкЖўЯѓЯоЃЉЃЎ
ЂйЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЂкЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЙ§xжсЩЯЕФЕуQЃЈдЕуГ§ЭтЃЉЃЌзїxжсЕФДЙЯпЗжБ№НЛХзЮяЯп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЪЧЗёДцдкЯпЖЮ
ЃЌЪЧЗёДцдкЯпЖЮ![]() ЃЈiЃЌjЮЊе§ећЪ§ЃЉЃЌЪЙ
ЃЈiЃЌjЮЊе§ећЪ§ЃЉЃЌЪЙ![]() ЃЌШєДцдкЃЌЧѓГіiЃЋjЕФзюаЁжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧѓГіiЃЋjЕФзюаЁжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћНЋЁїABCгыЁїDEFИїЗжИюГЩСНИіШ§НЧаЮЃЌЧвЁїABCЫљЗжЕФСНИіШ§НЧаЮгыЁїDEFЫљЗжЕФСНИіШ§НЧаЮЗжБ№ЖдгІЯрЫЦЃЌФЧУДГЦЁїABCгыЁїDEFЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЃЌНЋУПЬѕЗжИюЯпГЦЮЊЁАНќЫЦЗжИюЯпЁБЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌдкRtЁїABCКЭRtЁїDEFжаЃЌЁЯCЃНЁЯFЃН90ЁуЃЌЁЯAЃН30ЁуЃЌЁЯDЃН40ЁуЃЌЧыХаЖЯетСНИіШ§НЧаЮЪЧЗёЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЃПШчЙћЪЧЃЌЧыжБНгдкЭМ1жаЛГівЛзщЗжИюЯпЃЌВЂзЂУїЗжИюКѓЫљЕУСНИіаЁШ§НЧаЮШёНЧЕФЖШЪ§ЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉХаЖЯЯТСаУќЬтЪЧецУќЬтЛЙЪЧМйУќЬтЃЌШєЪЧецУќЬтЃЌЧыдкРЈКХФкДђЁАЁЬЁБЃЛШєЪЧМйУќЬтЃЌЧыдкРЈКХФкДђЁАЁСЁБЃЎ
ЂйШЮвтСНИіжБНЧШ§НЧаЮЖМЪЧЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЁЁ ЁЁЃЛ
ЂкСНИіЁАНќЫЦШ§НЧаЮЁБжЛгаЮЈвЛЕФЁАНќЫЦЗжИюЯпЁБЁЁ ЁЁЃЛ
ЂлШчЙћСНИіШ§НЧаЮжагавЛИіНЧЯрЕШЃЌФЧУДетСНИіШ§НЧаЮвЛЖЈЪЧЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЁЁ ЁЁЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌвбжЊЁїABCгыЁїDEFжаЃЌЁЯAЃНЁЯDЃН15ЁуЃЌЁЯBЃН45ЁуЃЌЁЯEЃН60ЁуЃЌЧвBCЃНEFЃН![]()
![]() ЃЌХаЖЯетСНИіШ§НЧаЮЪЧЗёЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЃПШчЙћЪЧЃЌЧыдкЭМ2жаЛГіВЛЭЌЮЛжУЕФЁАНќЫЦЗжИюЯпЁБЃЌВЂжБНгЗжБ№аДГіЁАНќЫЦЗжИюЯпЁБЕФКЭЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЃЌХаЖЯетСНИіШ§НЧаЮЪЧЗёЛЅЮЊЁАНќЫЦШ§НЧаЮЁБЃПШчЙћЪЧЃЌЧыдкЭМ2жаЛГіВЛЭЌЮЛжУЕФЁАНќЫЦЗжИюЯпЁБЃЌВЂжБНгЗжБ№аДГіЁАНќЫЦЗжИюЯпЁБЕФКЭЃЛШчЙћВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
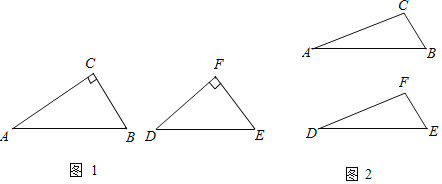
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com