【题目】欧拉（Euler，1707年~1783年）为世界著名的数学家、自然科学家，他在数学、物理、建筑、航海等领域都做出了杰出的贡献．他对多面体做过研究，发现多面体的顶点数（Vertex）、棱数E（Edge）、面数F（Flat surface）之间存在一定的数量关系，给出了著名的欧拉公式．
（1）观察下列多面体，并把下表补充完整：
名称 | 三棱锥 | 三棱柱 | 正方体 | 正八面体 |
图形 |
|
|
|
|
顶点数V | 4 | 6 | 8 | |
棱数E | 6 | 12 | ||
面数F | 4 | 5 | 8 |
（2）分析表中的数据，你能发现V、E、F之间有什么关系吗？请写出关系式：____________________________．
科目：初中数学 来源： 题型：
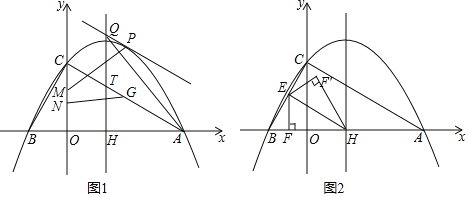
【题目】如图1，抛物线y
2
与x轴相交于A、B两点（点A在点B的右侧），与y轴相交于点C，对称轴与x轴相交于点H，与AC相交于点T．
（1）点P是线段AC上方抛物线上一点，过点P作PQ∥AC交抛物线的对称轴于点Q，当△AQH面积最大时，点M、N在y轴上（点M在点N的上方），MN
，点G在直线AC上，求PM+NG
GA的最小值．
（2）点E为BC中点，EF⊥x轴于F，连接EH，将△EFH沿EH翻折得△EF'H，如图所示2，再将△EF'H沿直线BC平移，记平移中的△EF'H为△E'F″H'，在平移过程中，直线E'H'与x轴交于点R，则是否存在这样的点R，使得△RF'H'为等腰三角形？若存在，求出R点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
，
，
，…，
（n为正整数），点A(0，1)．
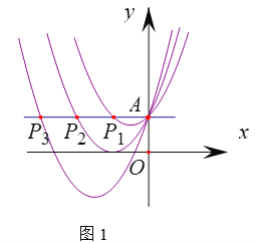
（1）如图1，过点A作y轴垂线，分别交抛物线
，
，
，…，
于点
，
，
，…，
（和点A不重合）．
①求
的长．
②求
的长．
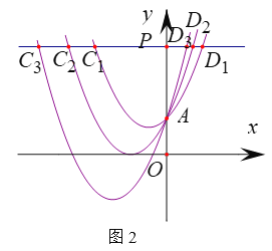
（2）如图2，点P从点A出发，沿y轴向上运动，过点P作y轴的垂线，交抛物线于点
，
，交抛物线于点
，
，交抛物线于点
，
，……，交抛物线于点
，
（在第二象限）．
①求
的值．
②求
的值．
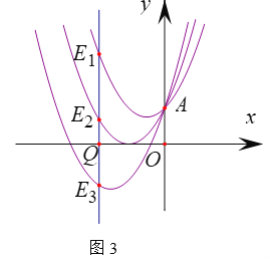
（3）过x轴上的点Q（原点除外），作x轴的垂线分别交抛物线，，，…，于点
，
，
，…，
，是否存在线段
（i，j为正整数），使
，若存在，求出i＋j的最小值；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
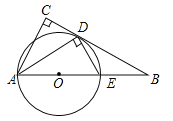
【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径．
（1）判断BC与⊙O的位置关系，并证明你的结论；
（2）求证：△ABD∽△DBE；
（3）若cosB=
，AE=4，求CD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
交x轴于
，
两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作
轴，交抛物线于点P，交BC于点Q．
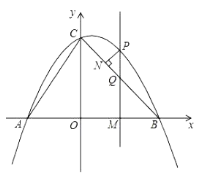
（1）求抛物线的表达式；
（2）过点P作
，垂足为点N．设M点的坐标为
，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？
（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
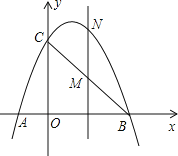
【题目】如图，已知抛物线经过点A（﹣1，0）、B（3，0）、C（0，3）三点．
（1）求抛物线的解析式．
（2）点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长．
（3）在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果将△ABC与△DEF各分割成两个三角形，且△ABC所分的两个三角形与△DEF所分的两个三角形分别对应相似，那么称△ABC与△DEF互为“近似三角形”，将每条分割线称为“近似分割线”．
（1）如图1，在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，∠A＝30°，∠D＝40°，请判断这两个三角形是否互为“近似三角形”？如果是，请直接在图1中画出一组分割线，并注明分割后所得两个小三角形锐角的度数；若不是，请说明理由．
（2）判断下列命题是真命题还是假命题，若是真命题，请在括号内打“√”；若是假命题，请在括号内打“×”．
①任意两个直角三角形都是互为“近似三角形” ；
②两个“近似三角形”只有唯一的“近似分割线” ；
③如果两个三角形中有一个角相等，那么这两个三角形一定是互为“近似三角形” ．
（3）如图2，已知△ABC与△DEF中，∠A＝∠D＝15°，∠B＝45°，∠E＝60°，且BC＝EF＝
，判断这两个三角形是否互为“近似三角形”？如果是，请在图2中画出不同位置的“近似分割线”，并直接分别写出“近似分割线”的和；如果不是，请说明理由．
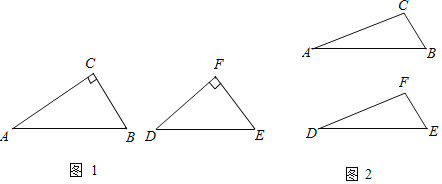
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．
（1）求证：BG=DE；
（2）若E为AD中点，FH=2，求菱形ABCD的周长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
