
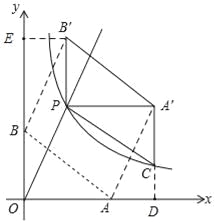
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

【答案】(1)k1=2,k2=8;(2)![]() ;(3)22
;(3)22
【解析】试题分析:(1)把点P(2,4)代入直线y=k1x,把点P(2,4)代入双曲线y=![]() ,可得k1与k2的值;
,可得k1与k2的值;
(2)根据平移的性质,求得C(6,![]() ),再运用待定系数法,即可得到直线PC的表达式;
),再运用待定系数法,即可得到直线PC的表达式;
(3)延长A'C交x轴于D,过B'作B'E⊥y轴于E,根据△AOB≌△A'PB',可得线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积,据此可得线段AB扫过的面积.
试题解析:(1)把点P(2,4)代入直线y=k1x,可得4=2k1,
∴k1=2,
把点P(2,4)代入双曲线y=![]() ,可得k2=2×4=8;
,可得k2=2×4=8;
(2)∵A(4,0),B(0,3),
∴AO=4,BO=3,
如图,延长A'C交x轴于D,
由平移可得,A'P=AO=4,
又∵A'C∥y轴,P(2,4),
∴点C的横坐标为2+4=6,
当x=6时,y=![]() =
=![]() ,即C(6,
,即C(6,![]() ),
),
设直线PC的解析式为y=kx+b,
把P(2,4),C(6,![]() )代入可得
)代入可得
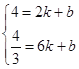 ,解得
,解得 ,
,
∴直线PC的表达式为y=﹣![]() x+
x+![]() ;
;
(3)如图,延长A'C交x轴于D,
由平移可得,A'P∥AO,
又∵A'C∥y轴,P(2,4),
∴点A'的纵坐标为4,即A'D=4,
如图,过B'作B'E⊥y轴于E,
∵PB'∥y轴,P(2,4),
∴点B'的横坐标为2,即B'E=2,
又∵△AOB≌△A'PB',
∴线段AB扫过的面积=平行四边形POBB'的面积+平行四边形AOPA'的面积=BO×B'E+AO×A'D=3×2+4×4=22.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22 015+22 016的值.
解:设S=1+2+22+23+24+…+22 015+22 016, ①
将等式两边同时乘2,得2S=2+22+23+24+25+…+22 016+22 017, ②
②-①,得2S-S=22 017-1,即S=22 017-1,
所以1+2+22+23+24+…+22 015+22 016=22 017-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+29+210;
(2)1+3+32+33+34+…+3n-1+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
一等奖 | 二等奖 | 三等奖 |
1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:

(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A、B两点,与
相交于A、B两点,与![]() 轴交于点M,M、N关于
轴交于点M,M、N关于![]() 轴对称,连接AN、BN.
轴对称,连接AN、BN.

(1)①求A、B的坐标;
②求证:∠ANM=∠BNM;
(2)如图,将题中直线![]() 变为
变为![]() ,抛物线
,抛物线![]() 变为
变为![]() ,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com