
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A、B两点,与
相交于A、B两点,与![]() 轴交于点M,M、N关于
轴交于点M,M、N关于![]() 轴对称,连接AN、BN.
轴对称,连接AN、BN.

(1)①求A、B的坐标;
②求证:∠ANM=∠BNM;
(2)如图,将题中直线![]() 变为
变为![]() ,抛物线
,抛物线![]() 变为
变为![]() ,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.

【答案】(1)①(-![]() ,
,![]() ),( 1,2)②证明见解析(2)∠ANM=∠BNM成立
),( 1,2)②证明见解析(2)∠ANM=∠BNM成立
【解析】
试题分析:(1)①联立直线和抛物线解析式可求得A、B两点的坐标;②过A作AC⊥y轴于C,过B作BD⊥y轴于D,可分别求得∠ANM和∠BNM的正切值,可证得结论;
(2)当k=0时,由对称性可得出结论;当k≠0时,过A作AE⊥y轴于E,过B作BF⊥y轴于F,设A![]() 、B
、B![]() ,联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得
,联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得![]() ,则可证明Rt△AEN∽Rt△BFN,可得出结论.
,则可证明Rt△AEN∽Rt△BFN,可得出结论.
试题解析: (1)①由已知得2x2=x+1,解得x=-![]() 或x=1,
或x=1,
当x=-![]() 时,y=
时,y=![]() ,当x=1时,y=2,
,当x=1时,y=2,
∴A、B两点的坐标分别为(-![]() ,
,![]() ),( 1,2);
),( 1,2);
②如图1,过A作AC⊥y轴于C,过B作BD⊥y轴于D,

由①及已知有A(-![]() ,
,![]() ),B( 1,2),且OM=ON=1,
),B( 1,2),且OM=ON=1,
∴tan∠ANM=![]() =
= ,tan∠BNM
,tan∠BNM![]() =
=![]() ,
,
∴tan∠ANM=tan∠BNM,
∴∠ANM=∠BNM;
(2)∠ANM=∠BNM成立,
①当k=0,△ABN是关于y轴的轴对称图形,
∴∠ANM=∠BNM;
②当k≠0,根据题意得:OM=ON=b,设A![]() 、B
、B![]() .
.
如图2,过A作AE⊥y轴于E,过B作BF⊥y轴于F,

由题意可知:ax2=kx+b,即ax2﹣kx﹣b=0,
∴![]() ,
,![]() ,
,
∵![]() =
=![]() =
=![]() =
=![]() =
= =0∴
=0∴![]() ,
,
∴Rt△AEN∽Rt△BFN,
∴∠ANM=∠BNM.


科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排![]() 名工人采摘蓝莓,剩下的工人加工蓝莓.
名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为![]() 元,求
元,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,Rt△PAB的直角顶点P(3,4)在函数y=![]() (x>0)的图象上,顶点A、B在函数y=
(x>0)的图象上,顶点A、B在函数y=![]() (x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA﹣S△PAB.
(x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA﹣S△PAB.
①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用2种方法表示可得一个等式,求等式。
(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.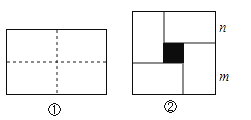
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段CF是由线段AB平移得到的:点A(﹣2,3)的对应点为C(1,2):则点B(a,b)的对应点F的坐标为( )
A. (a+3,b+1)B. (a+3,b﹣1)C. (a﹣3,b+1)D. (a﹣3,b﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)直接写出关于![]() 的一元二次方程
的一元二次方程![]() 的一个根;
的一个根;
(2)证明:抛物线![]() 的顶点
的顶点![]() 在第三象限;
在第三象限;
(3)直线![]() 与
与![]() 轴分别相交于
轴分别相交于![]() 两点,与抛物线
两点,与抛物线![]() 相交于
相交于![]() 两点.设抛物线
两点.设抛物线![]() 的对称轴与
的对称轴与![]() 轴相交于
轴相交于![]() ,如果在对称轴左侧的抛物线上存在点
,如果在对称轴左侧的抛物线上存在点![]() ,使得
,使得![]() 与
与![]() 相似.并且
相似.并且![]() ,求此时抛物线的表达式.
,求此时抛物线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+2交y轴于点A1 , 在x轴正方向上取点B1 , 使OB1=0A1;过点B1作A2B1⊥x轴,交l于点A2 , 在x轴正方向上取点B2 , 使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3 , 在x轴正方向上取点B3 , 使B2B3=B2A3记△OA1B1面积为S1,△B1A2B2面积为S2 , △B2A3B3面积为S3 , …则S2018等于.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com