
【题目】如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由. 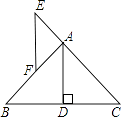
【答案】解:EF⊥BC,理由为: 证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵AE=AF,
∴∠E=∠EFA,
∵∠BAC=∠E+∠EFA=2∠EFA,
∴∠EFA=∠BAD,
∴EF∥AD,
∵AD⊥BC,
∴EF⊥BC,
则EF与BC的位置关系是垂直.
【解析】EF与BC垂直,理由为:由三角形ABC为等腰三角形且AD为底边上的高,利用三线合一得到AD为角平分线,再由AE=AF,利用等边对等角得到一对角相等,利用外角性质得到一对内错角相等,利用内错角相等两直线平行得到EF与AD平行,进而确定出EF与BC垂直.
【考点精析】根据题目的已知条件,利用等腰三角形的性质的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为 . 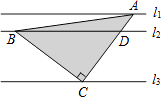
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一道题,已知线段AB=a,在直线AB上取一点C,使BC=b(a>b),点M,N分别是线段AB,BC的中点,求线段MN的长.对这道题,小善同学的答案是7,小昌同学的答案是3.老师说他们的结果都没错,如图,则依次可得到a的值是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A、B两点在数轴上所表示的数分别为a、b,则A、B两点间的距离可记为|a﹣b|:
(1)如图:若A、B两点在数轴上所表示的数分别为﹣2、4,求A、B两点的距离为;![]()
(2)若A,B两点分别以每秒3个单位长度和每秒1个单位长度的速度同时沿数轴正方向运动,设运动时间为t秒,解答下列问题:
①运动t秒后,A点所表示的数为 , B点所表示的数为;(答案均用含t的代数式表示)
②当t为何值时,A、B两点的距离为4?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
根据联合国《人口老龄化及其社会经济后果》中提到的标准,当一个国家或地区65岁及以上老年人口数量占总人口比例超过7%时,意味着这个国家或地区进入老龄化。从经济角度,一般可用“老年人口抚养比”来反映人口老龄化社会的后果。所谓“老年人口抚养比”是指某范围人口中,老年人口数(65岁及以上人口数)与劳动年龄人口数(15-64岁人口数)之比,通常用百分比表示,用以表明每100名劳动年龄人口要负担多少名老年人。
以下是根据我国近几年的人口相关数据制作的统计图和统计表。
2011-2014年全国人口年龄分布图

2011-2014年全国人口年龄分布表
2011年 | 2012年 | 2013年 | 2014年 | |
0-14岁人口占总人口的百分比 | 16.4% | 16.5% | 16.4% | 16.5% |
15-64岁人口占总人口的百分比 | 74.5% | 74.1% | 73.9% | 73.5% |
65岁及以上人口占总人口的百分比 | m | 9.4% | 9.7% | 10.0% |
*以上图表中数据均为年末的数据。
根据以上材料解答下列问题:
(1)2011年末,我国总人口约为_______亿,全国人口年龄分布表中m的值为_______;
(2)若按目前我国的人口自然增长率推测,到2027年末我国约有14.60亿人。假设0-14岁人口占总人口的百分比一直稳定在16.5%,15-64岁的人口一直稳定在10亿,那么2027年末我国0-14岁人口约为_______亿,“老年人口抚养比”约为_______; (精确到1%)
(3)2016年1月1日起我国开始施行“全面二孩”政策,一对夫妻可生育两个孩子。在未来10年内,假设出生率显著提高,这_______(填“会”或“不会”)对我国的“老年人口抚养比”产生影响。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com