练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形中，，，为边上一点，将沿翻折，点落在点处，当为直角三角形时，________.

    【答案】3或6

    【解析】

    对直角中那个角是直角分三种情况讨论，再由折叠的性质和勾股定理可BE的长.

    解：如图，若∠AEF=90°

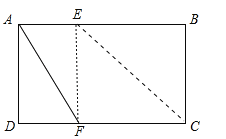
    ∵∠B=∠BCD=90°=∠AEF

    ∴四边形BCFE是矩形

    ∵将ABEC沿着CE翻折

    ∴CB=CF

    ∵四边形BCFE是正方形

    ∴BE=BC-AD=6，

    如图，若∠AFE=90°

    ∵将△BEC沿着CE翻折

    ∴CB=CF=6，∠B=∠EFC=90°，BE=EF

    ∵∠AFE+∠EFC=180°

    ∴点A，点F，点C三点共线

    ∴

    ∴AF=AC-CF=4

    ∵

    ∴

    ∴BE=3，

    若∠EAF=90°，

    ∵CD=8> CF=6

    ∴点F不可能落在直线AD上

    ∴.不存在∠EAF=90

    综上所述：BE=3或6

    故答案为：3或6

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，是等边三角形，是边上的一点，连接，把绕着点逆时针旋转，得到，连接，若，，则的周长是（ ）

    A.16B.15C.13D.12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a、b、c是正数，下列各式，从左到右的变形不能用如图验证的是（　　）

    A. （b+c）2＝b2+2bc+c2

    B. a（b+c）＝ab+ac

    C. （a+b+c）2＝a2+b2+c2+2ab+2bc+2ac

    D. a2+2ab＝a（a+2b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（提出问题）（1）如图1，已知AB∥CD，证明：∠1+∠EPF+∠2＝360°；

    （类比探究）（2）如图2，已知AB∥CD，设从E点出发的（n﹣1）条折线形成的n个角分别为∠1，∠2……∠n，探索∠1+∠2+∠3+……+∠n的度数可能在1700°至2000°之间吗？若有可能请求出n的值，若不可能请说明理由．

    （拓展延伸）（3）如图3，已知AB∥CD，∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O，若∠E1OEn＝m°．求∠2+∠3+∠4+…+∠（n﹣1）的度数．（用含m、n的代数式表示）

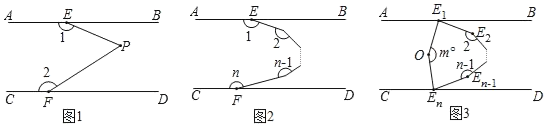
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】乌鲁木齐周边多地盛产草莓，今年某水果销售店在草莓销售旺季，以15元/kg 的成本价进50kg有机草莓，销售人员销售发现草莓损坏率为25%；

    （1）对于水果店来说完好的草莓实际成本价是多少元/kg?

    （2）按照这个实际成本设计销售单价，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量y（千克）与销售单价x（元）符合一次函数关系，如图是y与x的函数关系图象，设该水果销售店试销草莓获得的利润为W元，求W的最大值．

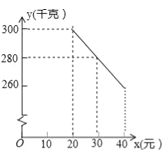
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在中，，点为直线上一动点(点不与点重合).以为边作正方形连接．

    观察猜想：

    （1）如图1，当点在线段上时，判断之间数量关系，并证明；

    　　　　　

    类比探究：

    （2）如图2，当点在线段的延长线上时，其他条件不变，请直接写出三条线段之间的关系；

    拓展延伸：

    （3）如图3，当点在线段的反向延长线上时，且点分别在直线的两侧，其他条件不变；

    ①请直接写出三条线段之间的关系；

    ②若正方形的边长为、对角线相交于点，连接，求的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】推理填空：已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4．求证：AD∥BE．

    证明：∵∠4=∠AFD（ ），

    ∵∠3=∠4（已知），

    ∴∠3=∠ （ ）.

    ∵∠1=∠2（已知）,

    ∴∠1+∠3=∠2+∠AFD（ ）.

    ∴∠D=∠ （ ）.

    ∴∠B=∠ （ ）.

    ∴∠________=∠ （ ）.

    ∴AD∥BE（ ）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线经过原点O及点A和点B．

    （1）求抛物线的解析式；

    （2）如图1，设抛物线的对称轴与x轴交于点C，将直线沿y轴向下平移n个单位后得到直线l，若直线l经过B点，与y轴交于点D，且与抛物线的对称轴交于点E．若P是抛物线上一点，且PB=PE，求点P的坐标；

    （3）如图2，将抛物线向上平移9个单位得到新抛物线，直接写出下列两个问题的答案：

    ①直线至少向上平移多少个单位才能与新抛物线有交点？

    ②新抛物线上的动点Q到直线的最短距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．

    （1）若他去买一瓶饮料，则他买到奶汁的概率是 ；

    （2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．

    查看答案和解析>>

    同步练习册答案