

���� ��1��������֪�����Ƴ���ABC�ǵ���ֱ�������Σ��õ�AB=BC������ת�����ʵõ�AD=AB����BAD=90�㣬�õ�AD=BC����BAD=��ABC=90�㣬�Ƴ�AD��BC�����ǵõ����ۣ�
��2���ɰ��߶�AC��C��˳ʱ����ת90��õ�CE���õ���ACE�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ���CAE=45�㣬�Ƴ�A��C��B��G�ĵ㹲Բ������Բ�ܽǶ������ɵõ����ۣ�
��3���ɣ�2��֪��CG��AE���õ�AG=EG=CG=2$\sqrt{2}$�����AC=4����G��GH����H����ֱ�������εõ�HG=HD=1�����ݹ��ɶ����õ�AH=$\sqrt{A{G}^{2}-H{G}^{2}}$=$\sqrt{7}$��Ȼ���ٸ��ݹ��ɶ������ɵõ����ۣ�
��� �⣺��1������Ϊ45��ʱ���ĵ�A��B��C��DΧ�ɵ��ı���Ϊƽ���ı��Σ�
�ߡ�ABC=90�㣬��BAC=45�㣬
���ABC�ǵ���ֱ�������Σ�
��AB=BC��
���߶�AB��A����ʱ����ת90��õ��߶�AD��
��AD=AB����BAD=90�㣬
��AD=BC����BAD=��ABC=90�㣬
��AD��BC��
���ı���ABCD��ƽ���ı��Σ�
��2���߰��߶�AC��C��˳ʱ����ת90��õ�CE��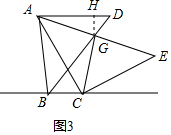
���ACE�ǵ���ֱ�������Σ�
���CAE=45�㣬
�ߡ�ABD=45�㣬��ABC=90�㣬
���CAG+��CBG=180�㣬
��A��C��B��G�ĵ㹲Բ��
���AGC=��ABC=90�㣬
��CG��AE��
��3���ɣ�2��֪��CG��AE��
��AG=EG=CG=2$\sqrt{2}$��
��AC=4��
��G��GH����H��
�ߡ�D=45�㣬DG=$\sqrt{2}$��
��HG=HD=1��
��AH=$\sqrt{A{G}^{2}-H{G}^{2}}$=$\sqrt{7}$��
��AB=AD=1+$\sqrt{7}$��
��BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{7}$-1��
�ʴ�Ϊ��$\sqrt{7}$-1��
���� ���⿼���˵���ֱ�������ε����ʣ���ת�����ʣ�ƽ���ı��ε��ж������ʣ��ĵ㹲Բ��Բ�ܽǶ�������ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
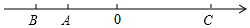 ��ͼ��a��b��c�ֱ���������A��B��C����Ӧ��ʵ�����Ի���$\sqrt{c^2}$+|a-b|+$\root{3}{��a+b��^{3}}$+|b-c|��
��ͼ��a��b��c�ֱ���������A��B��C����Ӧ��ʵ�����Ի���$\sqrt{c^2}$+|a-b|+$\root{3}{��a+b��^{3}}$+|b-c|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
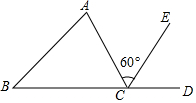 ��ͼ��CE�ǡ�ABC����ǡ�ACD��ƽ���ߣ�����A=85�㣬��ACE=60�㣬���B=��������
��ͼ��CE�ǡ�ABC����ǡ�ACD��ƽ���ߣ�����A=85�㣬��ACE=60�㣬���B=��������| A�� | 35�� | B�� | 95�� | C�� | 85�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com