
����Ŀ����������ǰϦ��ij���й���ij��Ʒ����Ʒ��ÿ�н�����40Ԫ�����й涨ÿ���ۼ۲�������45Ԫ����ÿ���ۼ�Ϊx(Ԫ)��ÿ���������y(��)��y��x��һ�εĺ�����ϵ�������г������ò����������±���
ÿ���ۼ�Ϊx(Ԫ) | 45 | 50 | 55 | �� |
ÿ���������y(��) | 450 | 400 | 350 | �� |
(1)�����y��x֮��ĺ�����ϵʽ��
(2)��ÿ���ۼ۶�Ϊ����Ԫʱ��ÿ�����۵�����P(Ԫ)�����������Ƕ��٣�
(3)��۲��Ź涨��������Ʒÿ���ۼ۲��ø���60Ԫ�����������Ҫÿ���ò�����5250Ԫ��������ô����ÿ����������������Ʒ���ٺУ�
���𰸡�(1)y����10x+900(45��x��90)��(2)��ÿ���ۼ۶�Ϊ65Ԫʱ��ÿ�����۵�����P(Ԫ)������������6250Ԫ��(3)������Ҫÿ���ò�����5250Ԫ��������ô����ÿ����������������Ʒ300�У�
��������
��1�����ݱ����е����ݺ��������ȷ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���������⣬�ɵ�ÿ�����۵�����![]() ���ۼ�
���ۼ�![]() ֮��ĺ�����ϵʽ��Ȼ���ٸ��ݶ��κ��������ֵ������ô𰸣�
֮��ĺ�����ϵʽ��Ȼ���ٸ��ݶ��κ��������ֵ������ô𰸣�
��3����������ͣ�1����2���еĺ�����ϵʽ��������ó���ÿ����������������Ʒ���ٺ�ʱ��ʹ�øó���ÿ���ò�����5250Ԫ������.
�⣺(1)��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() ��
��
![]() ��֮�ã�
��֮�ã�![]() ��
��
��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() ��
��
��2����������г�ÿ�����۵�����![]() ���ۼ�
���ۼ�![]() ֮��ĺ�����ϵʽ
֮��ĺ�����ϵʽ
��![]()
��![]()
�൱![]() ʱ��
ʱ��![]() ȡ�����ֵ����ʱ
ȡ�����ֵ����ʱ![]() ��
��
�𣺵�ÿ���ۼ۶�Ϊ65Ԫʱ��ÿ�����۵�����P(Ԫ)������������6250Ԫ��
(3)����������г�����ʽ
![]() ��
��
��֮�ã�![]() ��
��
�֡�![]() ��
��
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ȡ����Сֵ����ʱ
ȡ����Сֵ����ʱ![]() ��
��
�����������Ҫÿ���ò�����5250Ԫ��������ô����ÿ����������������Ʒ300�У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ӡ�����ӽ���������������ܵ����㷺��ע��ijУ�͡��л��Ļ��Ҵ��С����ط�Ϸ����У����ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ���������������ͳ��ͼ��
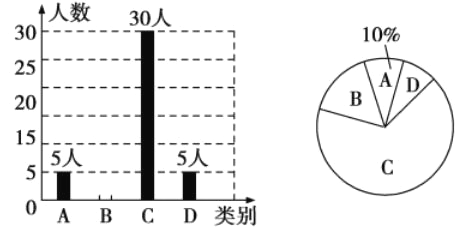
�������ͳ��ͼ���ṩ����Ϣ����������⣺
���ε����������Ϊ_____������ͳ��ͼ��C���������ε�Բ�ĽǶ���Ϊ_____��
��2����ȫ����ͳ��ͼ��
��3������У����ѧ��1800�ˣ���������������������Ƹ�Уѧ����A���� �ˣ�
��4���ڳ�ȡ��A��5���У��պ���3��Ů��2�����������������ȡ����ͬѧ��������ɫ���û���״ͼ�����б���������鵽������ѧ���Ա���ͬ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijС����һ�鳤Ϊ30m����Ϊ24m�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ480m2�������̵�֮�估�ܱ��п�����ȵ�����ͨ����������ͨ���Ŀ���Ϊxm������з���Ϊ_____��
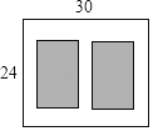
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O������Rt��ABC����P����Q�ֱ���ֱ�DZ�BC��б��AB�ϣ�PQ��AB����PQ���O���У���AC��2PQ����tan��B��ֵΪ��������
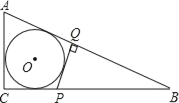
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
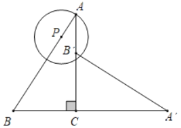
����Ŀ����ͼ����ABC�У���ACB��90����BC��3��cos��B��![]() ������ABC�Ƶ�C˳ʱ����ת90���õ���AB'C��PΪ�߶�AB�ϵĶ��㣬�Ե�PΪԲ�ģ�PA��Ϊ�뾶����P������P���A��B��C��һ�����ڵ�ֱ������ʱ����P�İ뾶Ϊ_____��
������ABC�Ƶ�C˳ʱ����ת90���õ���AB'C��PΪ�߶�AB�ϵĶ��㣬�Ե�PΪԲ�ģ�PA��Ϊ�뾶����P������P���A��B��C��һ�����ڵ�ֱ������ʱ����P�İ뾶Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
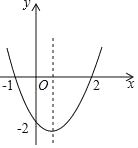
����Ŀ�����κ���y��ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0����4ac��b2����2a+b��0�����䶥������Ϊ��![]() ����2�����ݵ�x��
����2�����ݵ�x��![]() ʱ��y��x���������С����a+b+c��0���߷���ax2+bx+c����4��ʵ���⣬��ȷ������ ��
ʱ��y��x���������С����a+b+c��0���߷���ax2+bx+c����4��ʵ���⣬��ȷ������ ��
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����ɽ���½�C�����һ�������ﶥ��A������Ϊ63.4�㣬��ɽ�������ߵ�P���ٲ�øý����ﶥ��A������Ϊ53�㣮��֪BC=90�ף���B��C��D��ͬһ��ֱ���ϣ�ɽ���¶�i=5:12.
��1�����������λ�õ�P��Ǧֱ�߶ȣ��������ȷ��0.1�ף�
��2������˴�����λ�õ�P�ߵ�������ײ�B���·�̣������ȷ��0.1�ף�
���������ĸ߶Ⱥ��Բ��ƣ��ο����ݣ�tan53���![]() ��tan63.5���2��
��tan63.5���2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
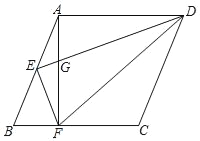
����Ŀ����ͼ����֪����ABCD����E��AB���е㣬AF��BC�ڵ�F������EF��ED��DF��DE��AF�ڵ�G����AE2��EGED��
(1)��֤��DE��EF��
(2)��֤��BC2��2DFBF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
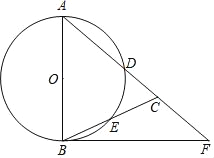
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������O���ֱ�AC��BC�ڵ�D��E����F��AC���ӳ����ϣ��ҡ�A��2��CBF��
(1)��֤��BF���O���У�
(2)��BC��CF��4����BF�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com