
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
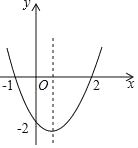
A. 3个 B. 4个 C. 5个 D. 6个
【答案】B
【解析】
根据二次函数的性质即可求出答案.
①由图象开口可知:a>0,c<0,
∵-![]() >0,
>0,
∴b<0,
∴abc>0,故①正确;
②由图象可知:△>0,
∴b2-4ac>0,
∴b2>4ac,故②正确;
③抛物线与x轴交于点A(-1,0),B(2,0),
∴抛物线的对称轴为:x=![]() =
=![]() ,
,
∴-![]() <1,
<1,
∴2a+b>0,
故③正确;
④由图象可知顶点坐标的纵坐标小于-2,故④错误;
⑤由③可知抛物线的对称轴为x=![]() ,
,
∴由图象可知:x<![]() 时,y随着x的增大而减小,
时,y随着x的增大而减小,
故⑤正确;
⑥由图象可知:x=1时,y<0,
∴a+b+c<0,
故⑥错误;
⑦由图象可知,顶点的纵坐标大于-4,
∴方程ax2+bx+c=-4无实数解,
故⑦错误;
故选B.


科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:∠CAD=∠B.
(2)若AC是∠BAD的平分线,sinB=![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
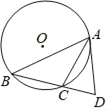
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春节”前夕,某超市购进某种品牌礼品,每盒进价是40元,超市规定每盒售价不得少于45元,设每盒售价为x(元),每天的销售量y(盒),y与x成一次的函数关系,经过市场调查获得部分数据如下表:
每盒售价为x(元) | 45 | 50 | 55 | … |
每天的销售量y(盒) | 450 | 400 | 350 | … |
(1)试求出y与x之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)物价部门规定:这种礼品每盒售价不得高于60元,如果超市想要每天获得不低于5250元的利润,那么超市每天至少销售这种礼品多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
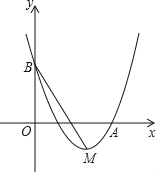
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对七年级300名学生进行了教学质量监测(满分100分),现从中随机抽取部分学生的成绩进行整理,并绘制成如图不完整的统计表和统计图:

注:60分以下为“不及格”,60~69分为“及格”,70~79分为“良好”,80分及以上为“优秀”
请根据以上信息回答下列问题:
(1)补全统计表和统计图;
(2)若用扇形统计图表示统计结果,则“良好”所对应扇形的圆心角为多少度?
(3)请估计该校七年级本次监测成绩为70分及以上的学生共有多少人?
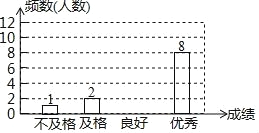
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com