
”¾ĢāÄæ”æijŠ£¶ŌĘßÄź¼¶300Ćūѧɜ½ųŠŠĮĖ½Ģѧ֏Įæ¼ą²ā£ØĀś·Ö100·Ö£©£¬ĻÖ“ÓÖŠĖ껜³éČ”²æ·ÖѧɜµÄ³É¼Ø½ųŠŠÕūĄķ£¬²¢»ęÖĘ³ÉČēĶ¼²»ĶźÕūµÄĶ³¼Ę±ķŗĶĶ³¼ĘĶ¼£ŗ

×¢£ŗ60·ÖŅŌĻĀĪŖ”°²»¼°øń”±£¬60”«69·ÖĪŖ”°¼°øń”±£¬70”«79·ÖĪŖ”°Į¼ŗĆ”±£¬80·Ö¼°ŅŌÉĻĪŖ”°ÓÅŠć”±
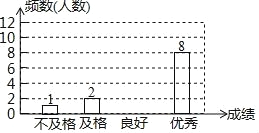
Ēėøł¾ŻŅŌÉĻŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©²¹Č«Ķ³¼Ę±ķŗĶĶ³¼ĘĶ¼£»
£Ø2£©ČōÓĆÉČŠĪĶ³¼ĘĶ¼±ķŹ¾Ķ³¼Ę½į¹ū£¬Ōņ”°Į¼ŗĆ”±Ėł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ¶ąÉŁ¶Č£æ
£Ø3£©Ēė¹Ą¼ĘøĆŠ£ĘßÄź¼¶±¾“Ī¼ą²ā³É¼ØĪŖ70·Ö¼°ŅŌÉĻµÄѧɜ¹²ÓŠ¶ąÉŁČĖ£æ
”¾“š°ø”æ£Ø1£©9£¬0.40£»£Ø2£©162”ć£»£Ø3£©255£®
”¾½āĪö”æ
£Ø1£©Ź×ĻČøł¾Ż²»ŗĻøńµÄČĖŹż¼°ĘµŹżĒóµĆ×ÜČĖŹż£¬Č»ŗó¼õČ„ĘäĖūø÷×éµÄʵŹż¼“æÉĒóµĆĮ¼ŗĆ×éµÄʵŹż£¬ÓĆʵŹż³żŅŌ×ÜČĖŹż¼“æÉĒóµĆʵĀŹ£»
£Ø2£©ÓĆĮ¼ŗƵÄʵĀŹ³ĖŅŌ360”ć¼“æÉĒóµĆĘä±ķŹ¾µÄÉČŠĪµÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø3£©ÓĆ×ÜČĖŹż³ĖŅŌ70·ÖŅŌÉĻµÄʵĀŹ¼“æÉĒóµĆČĖŹż£®
½ā£ŗ£Ø1£©½ā£ŗŅņĪŖ²»¼°øńµÄʵŹżĪŖ1£¬ĘµĀŹĪŖ0.05£¬ĖłŅŌ×ÜČĖŹżĪŖ1”Ā0.05=20ČĖ£¬ĖłŅŌĮ¼ŗƵÄʵŹżĪŖ20©1©2©8=9£¬ÓÅŠćµÄʵĀŹĪŖ8”Ā20=0.40£®
¹Ź“š°øĪŖ£ŗ9£¬0.40£»
Ķ³¼ĘĶ¼²¹Č«ĪŖ£ŗ
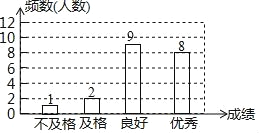
£Ø2£©0.45”Į360”ć=162”ć
“š£ŗ”°Į¼ŗĆ”±Ėł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ162”ć£»
£Ø3£©300”Į£Ø0.45+0.40£©=255£®
“š£ŗ¹Ą¼ĘøĆŠ£±¾“Ī¼ą²ā³É¼Ø70·Ö¼°ŅŌÉĻµÄѧɜ×ܹ²Ō¼ÓŠ255ČĖ£®
¹Ź“š°øĪŖ£ŗ£Ø1£©9£¬0.40£»£Ø2£©162”ć£»£Ø3£©255£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½¼Ņ²ŻŻ®²ÉÕŖŌ°µÄ²ŻŻ®Ę·ÖŹĻąĶ¬£¬ĻśŹŪ¼ŪøńŅ²ĻąĶ¬£®”°ĪåŅ»ĘŚ¼ä”±£¬Į½¼Ņ¾łĶĘ³öĮĖÓÅ»Ż·½°ø£¬¼×²ÉÕŖŌ°µÄÓÅ»Ż·½°øŹĒ£ŗÓĪæĶ½ųŌ°Šč¹ŗĀņ50ŌŖµÄĆÅʱ£¬²ÉÕŖµÄ²ŻŻ®ĮłÕŪÓÅ»Ż£»ŅŅ²ÉÕŖŌ°µÄÓÅ»Ż·½°øŹĒ£ŗÓĪæĶ½ųŌ°²»Šč¹ŗĀņĆÅʱ£¬²ÉÕŖŌ°µÄ²ŻŻ®³¬¹żŅ»¶ØŹżĮæŗ󣬳¬¹ż²æ·Ö“ņÕŪÓÅ»Ż£®ÓÅ»ŻĘŚ¼ä£¬ÉčijÓĪæĶµÄ²ŻŻ®²ÉÕŖĮæĪŖx£ØĒ§æĖ£©£¬ŌŚ¼×²ÉÕŖŌ°ĖłŠč×Ü·ŃÓĆĪŖ![]() £ØŌŖ£©£¬ŌŚŅŅ²ÉÕŖŌ°ĖłŠč×Ü·ŃÓĆĪŖ
£ØŌŖ£©£¬ŌŚŅŅ²ÉÕŖŌ°ĖłŠč×Ü·ŃÓĆĪŖ![]() £ØŌŖ£©£¬Ķ¼ÖŠÕŪĻßOAB±ķŹ¾
£ØŌŖ£©£¬Ķ¼ÖŠÕŪĻßOAB±ķŹ¾![]() ÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®
ÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®

£Ø1£©¼×”¢ŅŅĮ½²ÉÕŖŌ°ÓÅ»ŻĒ°µÄ²ŻŻ®ĻśŹŪ¼ŪøńŹĒĆæĒ§æĖ ŌŖ£»
£Ø2£©Ēó![]() ”¢
”¢![]() ÓėxµÄŗÆŹż±ķ“ļŹ½£»
ÓėxµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©ŌŚĶ¼ÖŠ»³ö![]() ÓėxµÄŗÆŹżĶ¼Ļ󣬲¢Š“³öŃ”Ōń¼×²ÉÕŖŌ°ĖłŠč×Ü·ŃÓĆ½ĻÉŁŹ±£¬²ŻŻ®²ÉÕŖĮæxµÄ·¶Ī§£®
ÓėxµÄŗÆŹżĶ¼Ļ󣬲¢Š“³öŃ”Ōń¼×²ÉÕŖŌ°ĖłŠč×Ü·ŃÓĆ½ĻÉŁŹ±£¬²ŻŻ®²ÉÕŖĮæxµÄ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
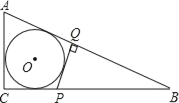
”¾ĢāÄæ”æČēĶ¼£¬”ŃOÄŚĒŠÓŚRt”÷ABC£¬µćP”¢µćQ·Ö±šŌŚÖ±½Ē±ßBC”¢Š±±ßABÉĻ£¬PQ”ĶAB£¬ĒŅPQÓė”ŃOĻąĒŠ£¬ČōAC£½2PQ£¬Ōņtan”ĻBµÄÖµĪŖ£Ø””””£©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
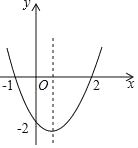
”¾ĢāÄæ”涞“ĪŗÆŹży£½ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ŅŌĻĀ½įĀŪ£ŗ¢Łabc£¾0£»¢Ś4ac£¼b2£»¢Ū2a+b£¾0£»¢ÜĘ䶄µć×ų±źĪŖ£Ø![]() £¬©2£©£»¢Żµ±x£¼
£¬©2£©£»¢Żµ±x£¼![]() Ź±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£»¢Ža+b+c£¾0£»¢ß·½³Ģax2+bx+c£½©4ÓŠŹµŹż½ā£¬ÕżČ·µÄÓŠ£Ø £©
Ź±£¬yĖęxµÄŌö“ó¶ų¼õŠ”£»¢Ža+b+c£¾0£»¢ß·½³Ģax2+bx+c£½©4ÓŠŹµŹż½ā£¬ÕżČ·µÄÓŠ£Ø £©
A. 3øö B. 4øö C. 5øö D. 6øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³ČĖŌŚÉ½ĘĀĘĀ½ÅC“¦²āµĆŅ»×ł½ØÖžĪļ¶„µćAµÄŃö½ĒĪŖ63.4”ć£¬ŃŲɽĘĀĻņÉĻ×ßµ½P“¦ŌŁ²āµĆøĆ½ØÖžĪļ¶„µćAµÄŃö½ĒĪŖ53”ć£®ŅŃÖŖBC=90Ć×£¬ĒŅB”¢C”¢DŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬É½ĘĀĘĀ¶Či=5:12.
£Ø1£©Ēó“ĖČĖĖłŌŚĪ»ÖƵćPµÄĒ¦Ö±øß¶Č£®£Ø½į¹ū¾«Č·µ½0.1Ć×£©
£Ø2£©Ēó“ĖČĖ“ÓĖłŌŚĪ»ÖƵćP×ßµ½½ØÖžĪļµ×²æBµćµÄĀ·³Ģ£Ø½į¹ū¾«Č·µ½0.1Ć×£©
£Ø²āĒćĘ÷µÄø߶ČŗöĀŌ²»¼Ę£¬²Īæ¼Źż¾Ż£ŗtan53”ć”Ö![]() £¬tan63.5”ć”Ö2£©
£¬tan63.5”ć”Ö2£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
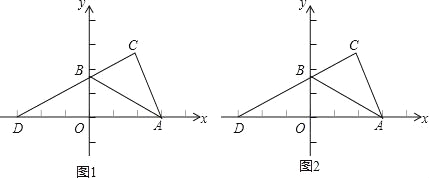
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷AOBŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ£ŗB£Ø0£¬![]() £©£¬µćAŌŚxÖįµÄÕż°ėÖįÉĻ£¬OA=3£¬”ĻBAD=30”ć£¬½«”÷AOBŃŲAB·ÕŪ£¬µćOµ½µćCµÄĪ»ÖĆ£¬Į¬½ÓCB²¢ŃÓ³¤½»xÖįÓŚµćD£®
£©£¬µćAŌŚxÖįµÄÕż°ėÖįÉĻ£¬OA=3£¬”ĻBAD=30”ć£¬½«”÷AOBŃŲAB·ÕŪ£¬µćOµ½µćCµÄĪ»ÖĆ£¬Į¬½ÓCB²¢ŃÓ³¤½»xÖįÓŚµćD£®
£Ø1£©ĒóµćDµÄ×ų±ź£»
£Ø2£©¶ÆµćP“ÓµćD³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲxÖįµÄÕż·½ĻņŌĖ¶Æ£¬µ±”÷PABĪŖÖ±½ĒČż½ĒŠĪŹ±£¬ĒótµÄÖµ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±”÷PABĪŖŅŌ”ĻPBAĪŖÖ±½ĒµÄÖ±½ĒČż½ĒŠĪŹ±£¬ŌŚyÖįÉĻŹĒ·ń“ęŌŚŅ»µćQŹ¹”÷PBQĪŖµČŃüČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öQµćµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
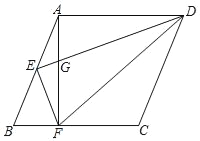
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĮāŠĪABCD£¬µćEŹĒABµÄÖŠµć£¬AF”ĶBCÓŚµćF£¬ĮŖ½įEF”¢ED”¢DF£¬DE½»AFÓŚµćG£¬ĒŅAE2£½EGED£®
(1)ĒóÖ¤£ŗDE”ĶEF£»
(2)ĒóÖ¤£ŗBC2£½2DFBF£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
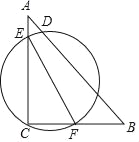
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½8£¬BC£½6£¬E£¬F·Ö±šŌŚ±ßAC£¬BC£¬ČōŅŌEFĪŖÖ±¾¶×÷Ō²¾¹żABÉĻijµćD£¬ŌņEF³¤µÄȔֵ·¶Ī§ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
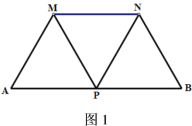
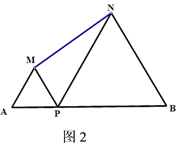
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬µćPŹĒĻ߶ĪABµÄÖŠµć£¬ĒŅAB=12£¬ĻÖ·Ö±šŅŌAP£¬BPĪŖ±ß£¬ŌŚABµÄĶ¬²ą×÷µČ±ß”÷MAPŗĶ”÷NBP£¬Į¬½įMN”£
(1)ĒėÖ»ÓĆ²»ŗ¬æĢ¶ČµÄÖ±³ßŌŚĶ¼1ÖŠÕŅµ½”÷MNPĶā½ÓŌ²µÄŌ²ŠÄO£¬²¢±£Įō×÷Ķ¼ŗŪ¼££»
(2)Čō½«”°µćPŹĒĻ߶ĪABµÄÖŠµć”±øijɔ°µćPŹĒĻ߶ĪABÉĻŅģÓŚ¶ĖµćµÄČĪŅāŅ»µć”±£¬ĘäÓąĢõ¼ž²»±ä(ČēĶ¼2)£¬ĒėÓĆĪÄ×ÖŠ“³ö”÷MNPĶā½ÓŌ²Ō²ŠÄOµÄĪ»ÖĆ£¬²¢Ēó³öøĆŌ²°ė¾¶µÄ×īŠ”Öµ.
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com