
【题目】如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为_____.
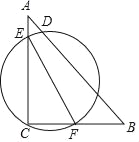
【答案】4.8≤EF≤10
【解析】
根据已知条件得到△ECF是直角三角形,推出点C在以EF为直径的圆上,设以EF为直径的圆的圆心为O,当⊙O于AB相切时,以EF为直径的圆经过AB上的唯一一点D,连接CD,则CD⊥AB,且CD过圆心,求得EF=CD=![]() =4.8,当⊙O经过A,B时,则EF=AB=10,于是得到结论.
=4.8,当⊙O经过A,B时,则EF=AB=10,于是得到结论.
∵∠C=90°,E,F分别在边AC,BC上,
∴△ECF是直角三角形,
∴点C在以EF为直径的圆上,
设以EF为直径的圆的圆心为O,
当⊙O于AB相切时,以EF为直径的圆经过AB上的唯一一点D,
连接CD,则CD⊥AB,且CD过圆心,
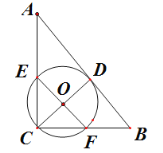
∴EF=CD,
∵∠C=90°,AC=8,BC=6,
∴AB=10,
∴EF=CD=![]() =4.8,
=4.8,
当⊙O经过A,B时,则EF=AB=10,
故EF长的取值范围为:4.8≤EF≤10.
故答案为:4.8≤EF≤10.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
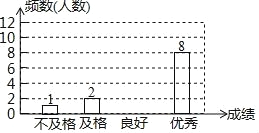
【题目】某校对七年级300名学生进行了教学质量监测(满分100分),现从中随机抽取部分学生的成绩进行整理,并绘制成如图不完整的统计表和统计图:

注:60分以下为“不及格”,60~69分为“及格”,70~79分为“良好”,80分及以上为“优秀”
请根据以上信息回答下列问题:
(1)补全统计表和统计图;
(2)若用扇形统计图表示统计结果,则“良好”所对应扇形的圆心角为多少度?
(3)请估计该校七年级本次监测成绩为70分及以上的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
有n个环环相扣的圆环形成一串线型链条,当只断开其中的k(k<n)个环,要求第一次取走一个环,以后每次都只能比前一次多得一个环,则最多能得到的环数n是多少呢?
问题探究:
为了找出n与k之间的关系,我们运用一般问题特殊化的方法,从特殊到一般,归纳出解决问题的方法.
探究一:k=1,即断开链条其中的1个环,最多能得到几个环呢?
当n=1,2,3时,断开任何一个环,都能满足要求,分次取走;
当n=4时,断开第二个环,如图①,第一次取走1环;第二次退回1环换取2环,得2个环;第三次再取回1环,得3个环;第四次再取另1环,得4个环,按要求分4次取走.
当n=5,6,7时,如图②,图③,图④方式断开,可以用类似上面的方法,按要求分5,6,7次取走.
当n=8时,如图⑤,无论断开哪个环,都不可能按要求分次取走.
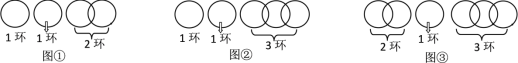
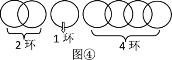
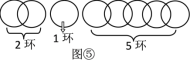
所以,当断开1个环时,从得到更多环数的角度考虑,把链条分成3部分,分别是1环、2环和4环,最多能得到7个环.
即当k=1时,最多能得到的环数n=1+2+4=1+2×3=1+2×(22-1)=7.
探究二:k=2,即断开链条其中的2个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑥方式断开,把链条分成5部分,按照类似探究一的方法,按要求分1,2,…23次取走.
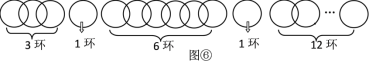
所以,当断开2个环时,把链条分成5部分,分别是1环、1环、3环、6环、12环,最多能得到23个环.
即当k=2时,最多能得到的环数n=1+1+3+6+12=2+3×7=2+3×(23-1)=23.
探究三:k=3,即断开链条其中的3个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑦方式断开,把链条分成7部分,按照类似前面探究的方法,按要求分1,2,…63次取走.
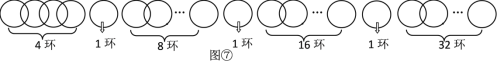
所以,当断开3个环时,从得到更多环数的角度考虑,把链条分成7部分,分别是1环、1环、1环、4环、8环、16环、32环,最多能得到63个环.
即当k=3时,最多能得到的环数n=1+1+1+4+8+16+32=3+4×15=3+4×(24-1)=63.
探究四:k=4,即断开链条其中的4个环,最多能得到几个环呢?
按照类似前面探究的方法,当断开4个环时,从得到更多环数的角度考虑,把链条分成 部分,分别为 ,最多能得到的环数n= .请画出如图⑥的示意图.
模型建立:
有n个环环相扣的圆环形成一串线型链条,断开其中的k(k<n)个环,从得到更多环数的角度考虑,把链条分成 部分,
分别是:1、1、1……1、k+1、 、……、 ,最多能得到的环数n = .
实际应用:
一天一位财主对雇工说:“你给我做两年的工,我每天付给你一个银环.不过,我用一串环环相扣的线型银链付你工钱,但你最多只能断开银链中的6个环.如果你无法做到每天取走一个环,那么你就得不到这两年的工钱,如果银链还有剩余,全部归你!你愿意吗?”
聪明的你是否可以运用本题的方法通过计算帮助雇工解决这个难题,雇工最多能得到总环数为多少环的银链?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且弧CB=弧CD,CE⊥DA交DA的延长线于点E.
(1)求证:∠CAB=∠CAE;
(2)求证:CE是⊙O的切线;
(3)若AE=1,BD=4,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
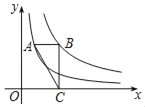
【题目】如图,点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
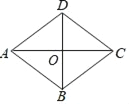
【题目】如图,已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,且对角线AC平分∠BCD,∠ACD=30°,BD=6.
(1)求证:△BCD是等边三角形;(2)求AC的长(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com