
����Ŀ�����������
��n��������۵�Բ���γ�һ��������������ֻ�Ͽ����е�k��k��n��������Ҫ���һ��ȡ��һ�������Ժ�ÿ�ζ�ֻ�ܱ�ǰһ�ζ��һ������������ܵõ��Ļ���n�Ƕ����أ�
����̽����
Ϊ���ҳ�n��k֮��Ĺ�ϵ����������һ���������⻯�ķ����������һ�㣬���ɳ��������ķ���.
̽��һ��k=1�����Ͽ��������е�1����������ܵõ��������أ�
��n=1,2,3ʱ���Ͽ��κ�һ��������������Ҫ�ִ�ȡ�ߣ�
��n=4ʱ���Ͽ��ڶ���������ͼ�٣���һ��ȡ��1�����ڶ����˻�1����ȡ2������2��������������ȡ��1������3���������Ĵ���ȡ��1������4��������Ҫ���4��ȡ�ߣ�
��n=5��6��7ʱ����ͼ�ڣ�ͼ�ۣ�ͼ�ܷ�ʽ�Ͽ�����������������ķ�������Ҫ���5,6,7��ȡ�ߣ�
��n=8ʱ����ͼ�ݣ����۶Ͽ��ĸ������������ܰ�Ҫ��ִ�ȡ�ߣ�
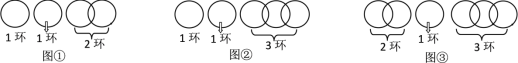
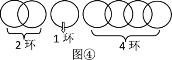
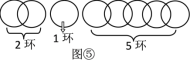
���ԣ����Ͽ�1����ʱ���ӵõ�������ĽǶȿ��ǣ��������ֳ�3���֣��ֱ���1����2����4��������ܵõ�7������
����k=1ʱ������ܵõ��Ļ���n=1+2+4=1+2��3=1+2����22-1��=7.
̽������k=2�����Ͽ��������е�2����������ܵõ��������أ�
�ӵõ�������ĽǶȿ��ǣ���ͼ��ʽ�Ͽ����������ֳ�5���֣���������̽��һ�ķ�������Ҫ���1,2����23��ȡ�ߣ�
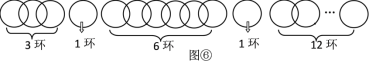
���ԣ����Ͽ�2����ʱ���������ֳ�5���֣��ֱ���1����1����3����6����12��������ܵõ�23������
����k=2ʱ������ܵõ��Ļ���n=1+1+3+6+12=2+3��7=2+3����23-1��=23.
̽������k=3�����Ͽ��������е�3����������ܵõ��������أ�
�ӵõ�������ĽǶȿ��ǣ���ͼ�߷�ʽ�Ͽ����������ֳ�7���֣���������ǰ��̽���ķ�������Ҫ���1,2����63��ȡ�ߣ�
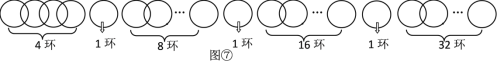
���ԣ����Ͽ�3����ʱ���ӵõ�������ĽǶȿ��ǣ��������ֳ�7���֣��ֱ���1����1����1����4����8����16����32��������ܵõ�63������
����k=3ʱ������ܵõ��Ļ���n=1+1+1+4+8+16+32=3+4��15=3+4����24-1��=63.
̽���ģ�k=4�����Ͽ��������е�4����������ܵõ��������أ�
��������ǰ��̽���ķ��������Ͽ�4����ʱ���ӵõ�������ĽǶȿ��ǣ��������ֳ� ���֣��ֱ�Ϊ ������ܵõ��Ļ���n= ���뻭����ͼ��ʾ��ͼ��
ģ�ͽ�����
��n��������۵�Բ���γ�һ�������������Ͽ����е�k��k��n���������ӵõ�������ĽǶȿ��ǣ��������ֳ� ���֣�
�ֱ��ǣ�1��1��1����1��k+1�� �������� ������ܵõ��Ļ���n = ��
ʵ��Ӧ�ã�
һ��һλ�����Թ�˵���������������Ĺ�����ÿ�츶����һ������������������һ��������۵������������㹤Ǯ���������ֻ�ܶϿ������е�6�����������������ÿ��ȡ��һ��������ô��͵ò���������Ĺ�Ǯ�������������ʣ�࣬ȫ�����㣡��Ը������
���������Ƿ�������ñ���ķ���ͨ��������������������⣬������ܵõ��ܻ���Ϊ���ٻ���������
���𰸡�̽���ģ����������ģ�ͽ��������������ʵ��Ӧ�ã�������ܵõ��ܻ���Ϊ895��������
��������
̽���ģ��������⻭��ͼ�η������ɴ˵ó���;
ģ�ͽ�������ǰ�浱n=1,2,3,4�����ɵã��Ӷ��ó����еĹ���;
ʵ��Ӧ�ã���k��6����n = k+(k+1)����2k+1-1�����㼴��.
̽���ģ�k=4�����Ͽ��������е�4����������ܵõ��������أ�
��������ǰ��̽���ķ��������Ͽ�4����ʱ���ӵõ�������ĽǶȿ��ǣ��������ֳ� �� ���֣��ֱ�Ϊ 1,1,1,1,5,10,20,40,80 ������ܵõ��Ļ���n= 1+1+1+1+5+10+20+40+80=4+5����25-1��=159 ��
ʾ��ͼ��
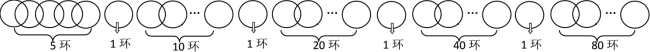
ģ�ͽ�������n��������۵�Բ���γ�һ�������������Ͽ����е�k��k��n���������ӵõ�������ĽǶȿ��ǣ��������ֳ� 2k+1 ���֣�
�ֱ��ǣ�1��1��1����1��k+1�� 2(k+1) �������� 2k(k+1) ������ܵõ��Ļ���n = k+(k+1)����2k+1-1�� ��.
ʵ��Ӧ�ã�
6+7����27-1��=895.
��Ϊ895�������������,
����Ը��.
�𣺹�����ܵõ��ܻ���Ϊ895��������.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
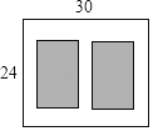
����Ŀ����ͼ��ijС����һ�鳤Ϊ30m����Ϊ24m�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ480m2�������̵�֮�估�ܱ��п�����ȵ�����ͨ����������ͨ���Ŀ���Ϊxm������з���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����ɽ���½�C�����һ�������ﶥ��A������Ϊ63.4�㣬��ɽ�������ߵ�P���ٲ�øý����ﶥ��A������Ϊ53�㣮��֪BC=90�ף���B��C��D��ͬһ��ֱ���ϣ�ɽ���¶�i=5:12.
��1�����������λ�õ�P��Ǧֱ�߶ȣ��������ȷ��0.1�ף�
��2������˴�����λ�õ�P�ߵ�������ײ�B���·�̣������ȷ��0.1�ף�
���������ĸ߶Ⱥ��Բ��ƣ��ο����ݣ�tan53���![]() ��tan63.5���2��
��tan63.5���2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
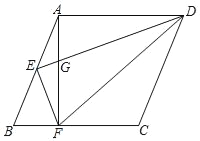
����Ŀ����ͼ����֪����ABCD����E��AB���е㣬AF��BC�ڵ�F������EF��ED��DF��DE��AF�ڵ�G����AE2��EGED��
(1)��֤��DE��EF��
(2)��֤��BC2��2DFBF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2��E��F�ֱ�ΪBC��CD���е㣬����AE��BF���ڵ�G������BCF��BF���ۣ��õ���BPF���ӳ�FP��AD�ڵ�M����BA���ӳ����ڵ�Q������BM�����н����У���AE��BF�� ��AE��BF����AQ��![]() ������MBF��60�㣮
������MBF��60�㣮
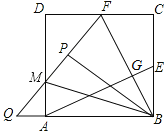
��ȷ�Ľ�����_____������ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C��90�㣬AC��8��BC��6��E��F�ֱ��ڱ�AC��BC������EFΪֱ����Բ����AB��ij��D����EF����ȡֵ��ΧΪ_____��
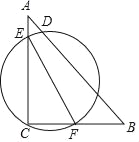
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2+bx+c��ͼ����x�ύ��A����3��0����B��1��0�����㣬��y�ύ�ڵ�C����OC��OA��
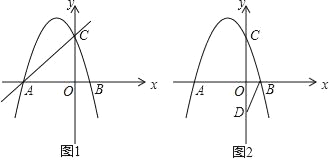
��1���������߽���ʽ��
��2����ֱ��AC�Ϸ�����������һ��M��y���ƽ���ߣ���ֱ��AC���ڵ�N����֪M��ĺ�����Ϊm�����ú�m��ʽ�ӱ�ʾMN�ij�����ACM�����S������MN�ij����ʱS��ֵ��
��3����ͼ2��D��0����2��������BD������OBD��ƽ���ڵ�ij�㣨��ΪP����ʱ����ת180��õ���O��B��D�䣬O��B��D�Ķ�Ӧ��ֱ�ΪO�䡢B�䡢D�䣮����B�䡢D������ǡ�������������ϣ�����ת���ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������O���ֱ�AC��BC�ڵ�D��E����F��AC���ӳ����ϣ��ҡ�A��2��CBF��
(1)��֤��BF���O���У�
(2)��BC��CF��4����BF�ij��ȣ�
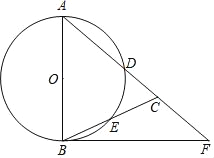
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. ��һö���ȵ����ӣ�����ֹͣת����5�㳯���DZ�Ȼ�¼�
B. ������ѩ�ĸ���Ϊ![]() ����ʾ�����а��춼����ѩ
����ʾ�����а��춼����ѩ
C. �ס�����������ͬ�����¸����10�Σ����dzɼ���ƽ������ͬ������ֱ���S��2=0.4��S��2=0.6���������ɼ����ȶ�
D. �˽�һ����籦��ʹ���������ʺ����ղ�ķ�ʽ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com