
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌBDЪЧжаЯпЃЌбгГЄBCжСEЃЌЪЙCEЃНCDЃЎ

ЃЈ1ЃЉжБНгаДГі![]() ЃНЁЁ ЃЛ
ЃНЁЁ ЃЛ
ЃЈ2ЃЉНЋЭМ1жаЕФЁїBDEШЦЕуBФцЪБеыа§зЊЕНШчЭМ2ЫљЪОЮЛжУЃЌСЌНгAEЃЌPЮЊAEЕФжаЕуЃЌСЌНгPDЃЌPCЃЌЬНОПЯпЖЮPDгыPCжЎМфЕФЙиЯЕЃЛ
ЃЈ3ЃЉНЋЭМ1жаЕФЁїBDEШЦЕуBЫГЪБеыа§зЊЃЌЪЙЕуDТфдкЯпЖЮBCЩЯЃЌСЌНгAEЃЌPЮЊAEжаЕуЃЌСЌНгPDЃЎШчЭМ3ЃЌШєABЃН2![]() ЃЌЧыжБНгаДГіPDЕФГЄЮЊЁЁ ЃЎ
ЃЌЧыжБНгаДГіPDЕФГЄЮЊЁЁ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉPCЃН![]() PDЃЌPDЁЭPCЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉPDЃН
PDЃЌPDЁЭPCЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉPDЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁЯDBCЃН30ЁуЃЌЭЦГіBCЃН2CDМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉНсТлPCЃН![]() PDЃЌPDЁЭPCЃЎШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎжЄУїЁїDBCЁеЁїMACЃЈSASЃЉЃЌЭЦГіЁїDCMЪЧЕШБпШ§НЧаЮЃЌМДПЩНтОіЮЪЬтЃЎ
PDЃЌPDЁЭPCЃЎШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎжЄУїЁїDBCЁеЁїMACЃЈSASЃЉЃЌЭЦГіЁїDCMЪЧЕШБпШ§НЧаЮЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌСЌНгPCЃЌЧѓГіCDЃЌРћгУЃЈ2ЃЉжаНсТлНтОіЮЪЬтМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1жаЃЌ
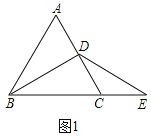
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌBDЪЧжаЯпЃЌ
ЁрBDЁЭACЃЌЁЯABDЃНЁЯDBCЃН30ЁуЃЌЁЯACBЃН60ЁуЃЌ
ЁрBCЃН2CDЃЌ
ЁпCDЃНCEЃЌ
ЁрBCЃН2ECЃЌ
Ёр![]() ЃН2ЃЎ
ЃН2ЃЎ
ЙЪД№АИЮЊ2ЃЎ
ЃЈ2ЃЉНтЃКНсТлPCЃН![]() PDЃЌPDЁЭPCЃЎ
PDЃЌPDЁЭPCЃЎ
РэгЩЃКШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎ
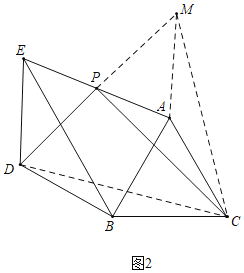
ЁпEPЃНPAЃЌЁЯEPDЃНЁЯAPMЃЌPDЃНPMЃЌ
ЁрЁїEPDЁеЁїAPMЃЈSASЃЉЃЌ
ЁрDEЃНAMЃЌЁЯDEPЃНЁЯPAMЃЌ
ЁпЁЯDBC+ЁЯACB+ЁЯCAE+ЁЯAED+ЁЯEDBЃН540ЁуЃЌ
ЁрЁЯDBC+ЁЯCAE+ЁЯAEDЃН540ЁуЉ120ЁуЉ60ЁуЃН360ЁуЃЌ
ЁпЁЯCAM+ЁЯCAE+ЁЯMAPЃН360ЁуЃЌ
ЁрЁЯCBDЃНЁЯCAMЃЌ
ЁпDEЃНDBЃНAMЃЌCBЃНCAЃЌ
ЁрЁїDBCЁеЁїMACЃЈSASЃЉЃЌ
ЁрCDЃНCMЃЌЁЯDCBЃНЁЯMACЃЌ
ЁрЁЯMCDЃНЁЯACBЃН60ЁуЃЌ
ЁрЁїDCMЪЧЕШБпШ§НЧаЮЃЌ
ЁпDPЃНPMЃЌ
ЁрPCЃН![]() PDЃЌPCЁЭPDЃЎ
PDЃЌPCЁЭPDЃЎ
ЃЈ3ЃЉНтЃКЂйШчЭМ3жаЃЌСЌНгPCЃЎ
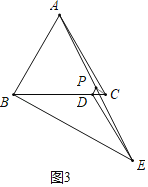
гЩЬтвтABЃНBCЃНACЃН2![]() ЃЌBDЃН3
ЃЌBDЃН3
ЁрCDЃНBCЉBDЃН2![]() Љ3ЃЌ
Љ3ЃЌ
гЩЃЈ2ЃЉПЩжЊЁЯCPDЃН90ЁуЃЌЁЯPCDЃН30ЁуЃЌ
ЁрPDЃН![]() CDЃН
CDЃН![]() Љ
Љ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ![]() Љ
Љ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
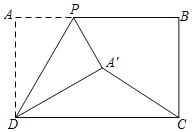
ЁОЬтФПЁПШчЭМЃЌЕуPЮЊОиаЮABCDЕФABБпЩЯвЛЖЏЕуЃЌНЋЁїADPбизХDPелЕўЃЌЕуAТфдкЕуA'ДІЃЌСЌНгCA'ЃЌвбжЊABЃН10ЃЌADЃН6ЃЌШєвдЕуPЃЌBЃЌCЃЌA'ЮЊЖЫЕуЕФЯпЖЮЃЈВЛдйСэЭтСЌНгЯпЖЮЃЉЙЙГЩЕФЭМаЮЮЊжБНЧШ§НЧаЮЛђЬиЪтЕФЦНааЫФБпаЮЪБЃЌAPЕФГЄЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓгыxжсЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєPЪЧЕкЫФЯѓЯоФкетИіЖўДЮКЏЪ§ЕФЭМЯѓЩЯШЮвтвЛЕуЃЌPHЁЭxжсгкЕуHЃЌгыBCНЛгкЕуMЃЌСЌНгPCЃЎ
ЂйЧѓЯпЖЮPMЕФзюДѓжЕЃЛ
ЂкЕБЁїPCMЪЧвдPMЮЊвЛбќЕФЕШбќШ§НЧаЮЪБЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћвЛдЊЖўДЮЗНГЬ![]() Тњзу
Тњзу![]() ЃЌФЧУДЮвУЧГЦетИіЗНГЬЮЊЁАЗяЛЫЁБЗНГЬЃЎвбжЊ
ЃЌФЧУДЮвУЧГЦетИіЗНГЬЮЊЁАЗяЛЫЁБЗНГЬЃЎвбжЊ![]() ЪЧЁАЗяЛЫЁБЗНГЬЃЌЧвгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђЯТСаНсТле§ШЗЕФЪЧ ( )
ЪЧЁАЗяЛЫЁБЗНГЬЃЌЧвгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђЯТСаНсТле§ШЗЕФЪЧ ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЊЩшМЦвЛБОЪщЕФЗтУцЃЌЗтУцГЄ27cmЃЌПэ21cmЃЌе§жабыЪЧвЛИігыећИіЗтУцГЄПэБШР§ЯрЭЌЕФГЄЗНаЮЃЌШчЙћвЊЪЙЫФжмЕФВЪЩЋБпГФЫљеМУцЛ§ЪЧЗтУцУцЛ§ЕФЫФЗжжЎвЛЃЌЩЯЁЂЯТБпГФЕШПэЃЌзѓЁЂгвБпГФЕШПэЃЌгІШчКЮЩшМЦЫФжмБпГФЕФПэЖШЃЈНсЙћБЃСєИљКХЃЉЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЁїABCФкНггкЁбOЃЌACЮЊЁбOЕФжБОЖЃЌЕуDЮЊгХЛЁBCЕФжаЕу
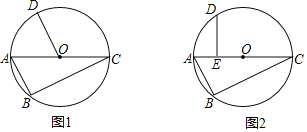
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгODЃЌЧѓжЄЃКABЁЮODЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуDзїDEЁЭACЃЌДЙзуЮЊEЃЎШєAEЃН3ЃЌBCЃН8ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDШЦзХЕуAЫГЪБеыа§зЊЕНе§ЗНаЮAEFGЃЌСЌНгCFЁЂDEЁЂGBЃЌШєDE=6ЃЌGB=4ЃЌдђЮхБпаЮAEFCDЕФУцЛ§ЮЊ_____.
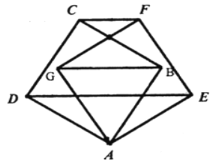
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЕФЭМЯѓОЙ§ЃЈЉ1ЃЌ0ЃЉЃЈ3ЃЌ0ЃЉСНЕуЃЌИјГіЕФЯТСа6ИіНсТлЃК
ЂйabЃМ0ЃЛ
ЂкЗНГЬax2+bx+cЃН0ЕФИљЮЊx1ЃНЉ1ЃЌx2ЃН3ЃЛ
Ђл4a+2b+cЃМ0ЃЛ
ЂмЕБxЃО1ЪБЃЌyЫцxжЕЕФдіДѓЖјдіДѓЃЛ
ЂнЕБyЃО0ЪБЃЌЉ1ЃМxЃМ3ЃЛ
Ђо3a+2cЃМ0ЃЎ
ЦфжаВЛе§ШЗЕФга_____ЃЎ
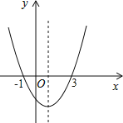
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌХзЮяЯпyЃНax2+bx+3гызјБъжсЗжБ№НЛгкЕуAЃЌBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ1ЃЌ0ЃЉЃЌЕуPЪЧЯпЖЮABЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїPABЕФУцЛ§зюДѓЃП
ЃЈ3ЃЉЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛЯпЖЮABгкЕуDЃЌдйЙ§ЕуPзїPEЁЮxжсНЛХзЮяЯпгкЕуEЃЌСЌНгDEЃЌЧыЮЪЪЧЗёДцдкЕуPЪЙЁїPDEЮЊЕШбќжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
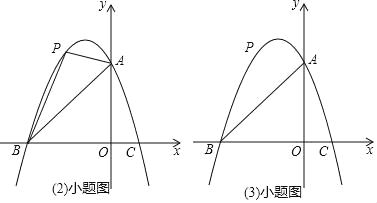
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com